题目内容
11.(1)抛物线y2=2px(p>0)上一点M到焦点的距离是a(a>$\frac{p}{2}$),则点M到准线的距离是a,点M的横坐标是a-$\frac{p}{2}$;(2)抛物线y2=12x上与焦点的距离等于9的点的坐标是(6,±6$\sqrt{2}$).
分析 抛物线y2=2px(p>0)上的点到焦点的距离等于到准线的距离,等于该点的横坐标加$\frac{p}{2}$,进而得到答案.
解答 解:(1)抛物线上的点到焦点的距离等于到准线的距离,
若抛物线y2=2px(p>0)上一点M到焦点的距离是a(a>$\frac{p}{2}$),
则点M到准线的距离也是a,
m的横坐标为a-$\frac{p}{2}$;
(2)抛物线y2=12x的准线方程为x=-3,
若抛物线y2=12x上点P到焦点的距离等于9,
则P点的横坐标为6,
则y=±6$\sqrt{2}$,
故P点的坐标为(6,±6$\sqrt{2}$);
故答案为:a,a-$\frac{p}{2}$,(6,±6$\sqrt{2}$).
点评 本题考查的知识点是抛物线的简单性质,熟练掌握抛物线的性质,是解答的关键.

练习册系列答案
相关题目
19.已知函数f(x)=(x-1)3+2014(x-1),等差数列{an}的前n项和为Sn,且f(a2)+f(a2014)=0,则S2015=( )
| A. | 4030 | B. | 4028 | C. | 2015 | D. | 2014 |
15.已知直线l经过点(4,0),且倾斜角为$\frac{3}{4}π$,圆M以$(\sqrt{2},\frac{π}{4})$为圆心,过极点.
(Ⅰ)求l与M的极坐标方程;
(Ⅱ)判断l与M的位置关系.
(Ⅰ)求l与M的极坐标方程;
(Ⅱ)判断l与M的位置关系.
16.若指数函数过点(2,4),则它的解析式为( )
| A. | y=2x | B. | y=(-2)x | C. | y=($\frac{1}{2}$)x | D. | y=(-$\frac{1}{2}$)x |
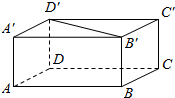 已知:如图的长方体AC′,求证:B′D′∥平面ABCD.
已知:如图的长方体AC′,求证:B′D′∥平面ABCD.