Question

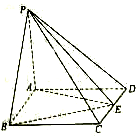如图，四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是矩形，AB=2，AD=3，PA=4，E为棱CD上一点，则三棱锥E-PAB的体积为

 

．

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：由V_E-PAB=V_P-ABE，利用等积法能求出三棱锥E-PAB的体积．

解答： 解：∵四棱锥P-ABCD中，PA⊥底面ABCD，
底面ABCD是矩形，AB=2，AD=3，PA=4，E为棱CD上一点，
∴S_△ABE=

1

2

×AB×AD=

1

2

×2×3=3，
∴三棱锥E-PAB的体积：
V_E-PAB=V_P-ABE=

1

3

×PA×S△ABE=

1

3

×4×3=4．
故答案为：4．

点评：本小题主要考查空间线面关系、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．