题目内容
已知f(x)=
x3+
x2+cx,g(x)=mx2+
x-9.当a=3,b=c=0时,若存在过点(1,0)的直线与曲线y=f(x)和y=g(x)都相切,求实数m的值.
| a |
| 3 |
| b |
| 2 |
| 15 |
| 4 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:分别求出f(x),g(x)的导数,设出切点,求得切线的斜率,运用两点的斜率公式和点在曲线上的条件,解方程即可得到m.
解答:
解:当a=3,b=c=0时,f(x)=x3,f′(x)=3x2,
g(x)的导数为g′(x)=2mx+
,
设过点(1,0)的切线与y=f(x)的切点为(e,f),与y=g(x)的切点为(s,t),
则3e2=2ms+
,
由e3=f,3e2=
=
,解得e=0或
,
则切线的方程为y=0或y=
(x-1).
若e=0,则ms=-
,且t=ms2+
s-9,
=0,
解得t=0,s=
,m=-
;
若e=
,则ms=
,且t=ms2+
s-9,
=
,
解得s=-
,m=-1.
综上可得,m=-
或m=-1.
g(x)的导数为g′(x)=2mx+
| 15 |
| 4 |
设过点(1,0)的切线与y=f(x)的切点为(e,f),与y=g(x)的切点为(s,t),
则3e2=2ms+
| 15 |
| 4 |
由e3=f,3e2=
| f |
| e-1 |
| e3 |
| e-1 |
| 3 |
| 2 |
则切线的方程为y=0或y=
| 27 |
| 4 |
若e=0,则ms=-
| 15 |
| 8 |
| 15 |
| 4 |
| t |
| s-1 |
解得t=0,s=
| 24 |
| 5 |
| 25 |
| 64 |
若e=
| 3 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
| t |
| s-1 |
| 27 |
| 4 |
解得s=-
| 3 |
| 2 |
综上可得,m=-
| 25 |
| 64 |
点评:本题考查导数的几何意义:函数在某点的导数即为曲线在该点处的切线的斜率,正确设出切点和求出导数,运用两点的斜率公式是解题的关键.

练习册系列答案
相关题目
函数f(x)=(x+1)|log2x|-1的零点个数为( )
| A、1 | B、2 | C、3 | D、4 |
若2°的圆心角所对的弧长为2m,那么这个弧所在圆的面积为( )
A、
| ||
B、
| ||
C、(
| ||
D、
|
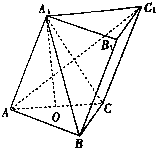 如图,在斜三棱柱ABC-A1B1C1中,点A1在底面ABC上的射影O是AC的中点,BC⊥AC,四边形BCC1B1是菱形,直线AB与平面ACC1A1所成的角为45°.
如图,在斜三棱柱ABC-A1B1C1中,点A1在底面ABC上的射影O是AC的中点,BC⊥AC,四边形BCC1B1是菱形,直线AB与平面ACC1A1所成的角为45°.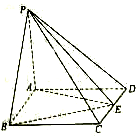 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是矩形,AB=2,AD=3,PA=4,E为棱CD上一点,则三棱锥E-PAB的体积为
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是矩形,AB=2,AD=3,PA=4,E为棱CD上一点,则三棱锥E-PAB的体积为