题目内容
已知数列{an}的通项公式an=
,试证明:1≤a1+a2+…+an<2.
| 1 |
| 2n-1 |
考点:数列递推式
专题:等差数列与等比数列
分析:由an=
≤
,得a1+a2+…+an≤1+
+
+…+
=2-
,由{2-
}是增数列,能证明1≤a1+a2+…+an<2.
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
解答:
证明:an=
≤
,
∴a1+a2+…+an≤1+
+
+…+
=
=2-
,
∵{2-
}是增数列,
∴当n=1时,2-
取最小值1,
∴1≤a1+a2+…+an<2.
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
∴a1+a2+…+an≤1+
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
=
1-
| ||
1-
|
=2-
| 1 |
| 2n-1 |
∵{2-
| 1 |
| 2n-1 |
∴当n=1时,2-
| 1 |
| 2n-1 |
∴1≤a1+a2+…+an<2.
点评:本题考查不等式的证明,是中档题,解题时要认真审题,注意放缩法的合理运用.

练习册系列答案
相关题目
已知△ABC和点M满足2
+
+
=0.若存在实m使得
+
=m
成立,则m=( )
| MA |
| MB |
| MC |
| AB |
| AC |
| AM |
| A、2 | B、3 | C、4 | D、5 |
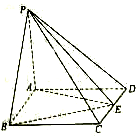 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是矩形,AB=2,AD=3,PA=4,E为棱CD上一点,则三棱锥E-PAB的体积为
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是矩形,AB=2,AD=3,PA=4,E为棱CD上一点,则三棱锥E-PAB的体积为