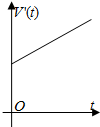题目内容
在△ABC中，若sinA：sinB：sinC=3：4：5，则cosB= ．
考点：余弦定理,正弦定理
专题：解三角形
分析：由已知设sinA=3t，sinB=4t，sinC=5t，∴由正弦定理可得a=6tR，b=8tR，c=10tR，由余弦定理即可求得cosB的值．
解答：
解：∵sinA：sinB：sinC=3：4：5，
∴设sinA=3t，sinB=4t，sinC=5t，
∴由正弦定理可得：
=
=
=2R，可得：a=6tR，b=8tR，c=10tR，
∴由余弦定理可得：cosB=
=
=
．
故答案为：
．
∴设sinA=3t，sinB=4t，sinC=5t，
∴由正弦定理可得：
| a |
| 3t |
| b |
| 4t |
| c |
| 5t |
∴由余弦定理可得：cosB=
| a2+c2-b2 |
| 2ac |
| t2R2(36+100-64) |
| 120t2R2 |
| 3 |
| 5 |
故答案为：
| 3 |
| 5 |
点评：本题主要考查了正弦定理，余弦定理在解三角形中的应用，属于基本知识的考查．
练习册系列答案
相关题目
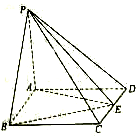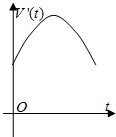
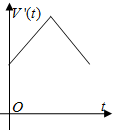
如图，四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是矩形，AB=2，AD=3，PA=4，E为棱CD上一点，则三棱锥E-PAB的体积为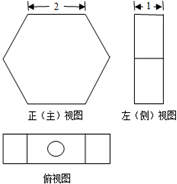
一容器的三视图（正视图是一正六边形）如图，现加入溶液，记溶液液面与容器底面的距离为t，溶液体积为V（t），则函数V（t）的导函数V′（t）的大致图形是（ ）
