题目内容
设p:f(x)=lnx+2x2+mx+1在(0,+∞)上是递增的,q:m≥-4,则p是q的 条件.
考点:必要条件、充分条件与充要条件的判断
专题:导数的概念及应用,简易逻辑
分析:结合函数单调性的性质,利用充分条件和必要条件的定义进行判断即可.
解答:
解:要使f(x)=lnx+2x2+mx+1在(0,+∞)内单调递增,则f′(x)≥0在(0,+∞)恒成立,
即f′(x)=
+4x+m≥0恒成立,
∴m≥-(
+4x)在(0,+∞)恒成立,
∵当x>0时,
+4x≥2
=2
=4,
∴-(
+4x)≤-4,即m≥-4,
∴p:m≥-4,
∵q:m≥-4,
∴p是q的充分必要条件.
故答案为:充要条件
即f′(x)=
| 1 |
| x |
∴m≥-(
| 1 |
| x |
∵当x>0时,
| 1 |
| x |
|
| 4 |
∴-(
| 1 |
| x |
∴p:m≥-4,
∵q:m≥-4,
∴p是q的充分必要条件.
故答案为:充要条件
点评:本题主要考查充分条件和必要条件的判断,利用函数单调性和导数之间的关系求出p的等价条件是解决本题的关键.

练习册系列答案
相关题目
把五个标号为1到5的小球全部放入标号为1到4的四个盒子中,不许有空盒且任意一个小球都不能放入标有相同标号的盒子中,则不同的放法有( )
| A、36种 | B、45种 |
| C、54种 | D、84种 |
已知△ABC和点M满足2
+
+
=0.若存在实m使得
+
=m
成立,则m=( )
| MA |
| MB |
| MC |
| AB |
| AC |
| AM |
| A、2 | B、3 | C、4 | D、5 |
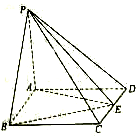 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是矩形,AB=2,AD=3,PA=4,E为棱CD上一点,则三棱锥E-PAB的体积为
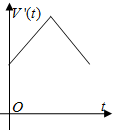
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是矩形,AB=2,AD=3,PA=4,E为棱CD上一点,则三棱锥E-PAB的体积为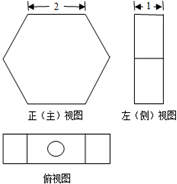 一容器的三视图(正视图是一正六边形)如图,现加入溶液,记溶液液面与容器底面的距离为t,溶液体积为V(t),则函数V(t)的导函数V′(t)的大致图形是( )
一容器的三视图(正视图是一正六边形)如图,现加入溶液,记溶液液面与容器底面的距离为t,溶液体积为V(t),则函数V(t)的导函数V′(t)的大致图形是( )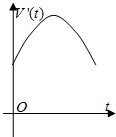

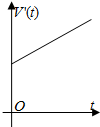
 如图是一个几何体的三视图,已知侧视图是一个等边三角形,根据图中尺寸(单位:cm),这个几何体的体积为
如图是一个几何体的三视图,已知侧视图是一个等边三角形,根据图中尺寸(单位:cm),这个几何体的体积为