题目内容
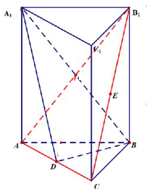 三棱柱中D、E为AC、B1C的中点,证明:
三棱柱中D、E为AC、B1C的中点,证明:(1)B1C∥平面A1BD;
(2)DE∥平面A1B1BA.
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:充分利用三角形的中位线得到线线平行,利用线面平行的判定定理可证.
解答:
证明:(1)如图设AB1与A1B相交于O,因为三棱柱中D为AC的中点,所以在△ACB1中,OD∥B1C,
又OD?平面A1BD,B1C?平面A1BD,
所以B1C∥平面A1BD;
(2)在△ACB1中三棱柱中D、E为AC、B1C的中点,所以DE∥AB1,
DE?平面A1B1BA,AB1?平面A1B1BA,
所以DE∥平面A1B1BA.
又OD?平面A1BD,B1C?平面A1BD,
所以B1C∥平面A1BD;
(2)在△ACB1中三棱柱中D、E为AC、B1C的中点,所以DE∥AB1,
DE?平面A1B1BA,AB1?平面A1B1BA,
所以DE∥平面A1B1BA.
点评:本题考查了线面平行的判定;利用三角形的中位线转化为线线平行,结合线面平行的判定定理可证.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
命题“?x0∈R,x02+x0+2<0”的否定是( )
| A、?x0∈R,x02+x0+2≥0 |
| B、?x∈R,x2+x+2≥0 |
| C、?x∈R,x2+x+2<0 |
| D、?x∈R,x2+x+2>0 |
已知tanθ=2,则
=( )
sin(
| ||
sin(
|
| A、2 | ||
| B、-2 | ||
| C、0 | ||
D、
|
与角
终边相同的角是( )
| 11π |
| 6 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|