题目内容
一个袋中有4个大小相同的小球,其中红球1个,白球2个,黑球1个,现从袋中有放回地取球,每次随机取一个,求:(Ⅰ)连续取两次都是白球的概率;
(Ⅱ)若取一个红球记2分,取一个白球记1分,取一个黑球记0分,连续取两次分数之和不小于2分的概率.
(Ⅱ)若取一个红球记2分,取一个白球记1分,取一个黑球记0分,连续取两次分数之和不小于2分的概率.
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题:概率与统计
分析:(I)利用列举法写出连续取两次的事件总数情况,共16种,从中算出连续取两次都是白球的种数,最后求出它们的比值即可;
(II)用列举法求出连续取二次的基本事件总数,从中数出连续取二次分数之和不小于2分的种数,求出它们的比值即为所求的概率.
(II)用列举法求出连续取二次的基本事件总数,从中数出连续取二次分数之和不小于2分的种数,求出它们的比值即为所求的概率.
解答:
解:(Ⅰ)连续取两次所包含的基本事件有:(红,红),(红,白1),(红,白2),(红,黑);(白1,红)(白1,白1)(白1,白2),(白1,黑);(白2,红),(白2,白1),(白2,白2),(白2,黑);(黑,红),(黑,白1),(黑,白2),(黑,黑),所以基本事件的总数16,
设事件A:连续取两次都是白球,则事件A所包含的基本事件有:
(白1,白1)(白1,白2),(白2,白1),(白2,白2)共4个,
所以P(A)=
=
,
(Ⅱ):设事件B:连续取两次分数之和不小于2分,( 则为2,3,4分)
设事件C:连续取两次分数之和为(2分)的情况有(红球1个,黑球1个),(白球2个),则P(C)=
=
设事件D:连续取两次分数之和为3分的情况有(红球1个,白球1个),则P(D)=
=
设事件E:连续取两次分数之和为(4分)的情况有(红球2个),P(E)=
,
故P(B)=P(C)+P(D)+P(E)=
设事件A:连续取两次都是白球,则事件A所包含的基本事件有:
(白1,白1)(白1,白2),(白2,白1),(白2,白2)共4个,
所以P(A)=
| 4 |
| 16 |
| 1 |
| 4 |
(Ⅱ):设事件B:连续取两次分数之和不小于2分,( 则为2,3,4分)
设事件C:连续取两次分数之和为(2分)的情况有(红球1个,黑球1个),(白球2个),则P(C)=
| 6 |
| 16 |
| 3 |
| 8 |
设事件D:连续取两次分数之和为3分的情况有(红球1个,白球1个),则P(D)=
| 4 |
| 16 |
| 1 |
| 4 |
设事件E:连续取两次分数之和为(4分)的情况有(红球2个),P(E)=
| 1 |
| 16 |
故P(B)=P(C)+P(D)+P(E)=
| 11 |
| 16 |
点评:本题考查概率的求法与运用,一般方法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
相关题目
若x、y满足不等式
,则(2x+y)2的最小值( )
|
| A、-4 | B、16 | C、4 | D、0 |
 如图,延长△ABC的边BC到D,若tanB=
如图,延长△ABC的边BC到D,若tanB=| 5 |
| 8 |
| 1 |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
 如图,已知 ABCD-A1B1C1D1是棱长为a的正方体,点E为AA1的中点,点F为CC1的中点,求证:EB∥FD1.
如图,已知 ABCD-A1B1C1D1是棱长为a的正方体,点E为AA1的中点,点F为CC1的中点,求证:EB∥FD1. 在平面四边形ABCD中,AD=1,CD=2,AB=3,cos∠CAD=
在平面四边形ABCD中,AD=1,CD=2,AB=3,cos∠CAD=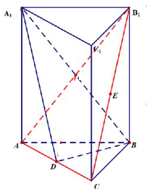 三棱柱中D、E为AC、B1C的中点,证明:
三棱柱中D、E为AC、B1C的中点,证明: