题目内容
命题“?x0∈R，x02+x0+2＜0”的否定是（ ）
| A、?x0∈R，x02+x0+2≥0 |
| B、?x∈R，x2+x+2≥0 |
| C、?x∈R，x2+x+2＜0 |
| D、?x∈R，x2+x+2＞0 |
考点：命题的否定
专题：简易逻辑
分析：直接利用特称命题的否定是全称命题写出结果即可．
解答：
解：因为特称命题的否定是全称命题，
所以命题“?x0∈R，x02+x0+2＜0”的否定是?x∈R，x2+x+2≥0．
故选：B．
所以命题“?x0∈R，x02+x0+2＜0”的否定是?x∈R，x2+x+2≥0．
故选：B．
点评：本题考查命题的否定特称命题与全称命题的否定关系，基本知识的考查．
练习册系列答案
相关题目
角α的中边上有点（-3，4）则cosα=（ ）
A、-
| ||
B、
| ||
C、
| ||
D、-
|
已知集合A={1，2}，则下列说法正确的是（ ）
| A、1⊆A | B、{1}∈A |
| C、A⊆{1} | D、Φ⊆A |
在同一直角坐标系中，直线y=ax与y=a+x的图象可能是（ ）
A、 |
B、 |
C、 |
D、 |
如图，四棱锥P-ABCD的底面是边长为1的正方形，PA⊥CD，PA=1，PD=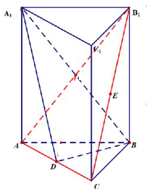
三棱柱中D、E为AC、B1C的中点，证明：