题目内容
已知函数f(x)=sinx.若f(x)+1≥ax+cosx在[0,π]上恒成立,则实数a的取值范围是 .
考点:三角函数的化简求值
专题:计算题,导数的综合应用
分析:先将不等式转化成函数利用导数,讨论a,进而即可求出a的取值范围.
解答:
解:设g(x)=sinx+1-ax-cosx,g′(x)=cosx-a+sinx=
sin(x+
)-a.
∵x∈[0,π],∴
sin(x+
)∈[-1,
].
当a≤-1时,g′(x)≥0在[0,π]上恒成立,
∴g(x)≥g(x)min=g(0)=0成立,
故a≤-1;
当a≥
时,g′(x)≤0在[0,π]上恒成立,g(x)=g(π)=2-πa≥0,得a≤
,无解.
当-1<a<
时,则存在x0∈(0,π]使得x∈(0,x0)时,g(x)是增函数,x∈(x0,π]时,g(x)是减函数,
故g(x)min=g(0),或g(x)min=g(π),
∴
,解得:a≤
,
故-1<a≤
.
综上所述:a≤
.
故答案为:a≤
.
| 2 |
| π |
| 4 |
∵x∈[0,π],∴
| 2 |
| π |
| 4 |
| 2 |
当a≤-1时,g′(x)≥0在[0,π]上恒成立,
∴g(x)≥g(x)min=g(0)=0成立,
故a≤-1;
当a≥
| 2 |
| 2 |
| π |
当-1<a<
| 2 |
故g(x)min=g(0),或g(x)min=g(π),
∴
|
| 2 |
| π |
故-1<a≤
| 2 |
| π |
综上所述:a≤
| 2 |
| π |
故答案为:a≤
| 2 |
| π |
点评:本题主要考察了导数的综合应用,三角函数的化简求值,考察了转化思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在同一直角坐标系中,直线y=ax与y=a+x的图象可能是( )
A、 |
B、 |
C、 |
D、 |
若x、y满足不等式
,则(2x+y)2的最小值( )
|
| A、-4 | B、16 | C、4 | D、0 |
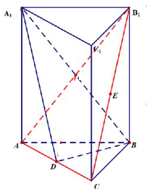 三棱柱中D、E为AC、B1C的中点,证明:
三棱柱中D、E为AC、B1C的中点,证明: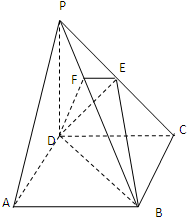 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F,求证:PF=
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F,求证:PF=