题目内容
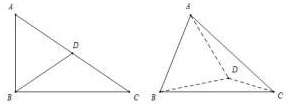
在直角△ABC中,∠ACB=30°,∠B=90°,D为AC中点(左图),将∠ABD沿BD折起,使得AB⊥CD(右图),则二面角A-BD-C的余弦值为( )

A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
考点:二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:由(1)的证明可得∠A′EF为二面角A-BD-C的平面角.过A作AO⊥面BCD,垂足为O.由于面AEF⊥面BCD,所以O在FE上,连BO交CD延长线于M,从而当AB⊥CD时,由三垂线定理的逆定理得BM⊥CM,由此可求得cos∠AEO=
,利用互补得出二面角A-BD-C的余弦值为-
.
| 1 |
| 3 |
| 1 |
| 3 |
解答:
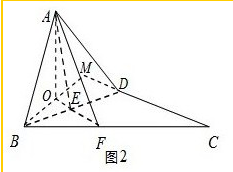
解:过A作AE⊥BD,在原图延长角BC与F,
过A作AO⊥面BCD,垂足为O.由于面AEF⊥面BCD,所以O在FE上,连BO交CD延长线于M,

∵在△ABC中,∠ACB=30°,∠B=90°,D为AC中点,
AB=
AC,BD=
AC,
∴△ABD为等边三角形,
∴BD⊥AE,BD⊥EF,
∴∠AEF为二面角A-BD-C的平面角,
过A作AO⊥面BCD,垂足为O,
∵面AEF⊥面BCD,
∴O在EF上,
理解BO交CD延长线于M,
当AB⊥CD时,由三垂线定理的逆定理可知:MB⊥CM,
∴O为翻折之前的三角形ABD的中心,
∴OE=
AE,
cos∠AEO=
,
∴cos∠AEF=-
,
故选:A
过A作AO⊥面BCD,垂足为O.由于面AEF⊥面BCD,所以O在FE上,连BO交CD延长线于M,


∵在△ABC中,∠ACB=30°,∠B=90°,D为AC中点,
AB=
| 1 |
| 2 |
| 1 |
| 2 |
∴△ABD为等边三角形,
∴BD⊥AE,BD⊥EF,
∴∠AEF为二面角A-BD-C的平面角,
过A作AO⊥面BCD,垂足为O,
∵面AEF⊥面BCD,
∴O在EF上,
理解BO交CD延长线于M,
当AB⊥CD时,由三垂线定理的逆定理可知:MB⊥CM,
∴O为翻折之前的三角形ABD的中心,
∴OE=
| 1 |
| 3 |
cos∠AEO=
| 1 |
| 3 |
∴cos∠AEF=-
| 1 |
| 3 |
故选:A
点评:本题以平面图形为载体,考查图形的翻折,关键是搞清翻折前后有关元素的变与不变,考查面面角,考查线面角,关键是正确作出相应的角

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=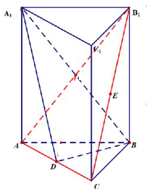 三棱柱中D、E为AC、B1C的中点,证明:
三棱柱中D、E为AC、B1C的中点,证明: