题目内容
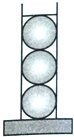圆柱形容器内盛有高度为12cm的水，若放入三个不同的球（球的半径与圆柱的底面半径相同）后，水恰好淹没最上面的球（如图所示），则球的半径是考点：球的体积和表面积,旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：设出球的半径，三个球的体积和水的体积之和，等于柱体的体积，求解即可．
解答：
解：设球半径为r，
则由3V球+V水=V柱可得：
3×
πr3+πr2×12=πr2×6r，
解得r=6．
故答案为：6．
则由3V球+V水=V柱可得：
3×
| 4 |
| 3 |
解得r=6．
故答案为：6．
点评：本题考查几何体的体积，考查学生空间想象能力，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
不等式x2+2x＜
+
对任意a，b∈（0，+∞）恒成立，则实数x的取值范围是（ ）
| a |
| b |
| 16b |
| a |
| A、hmax（x） |
| B、（-∞，-2）∪（0，+∞） |
| C、（-4，2） |
| D、（-∞，-4）∪（2，+∞） |
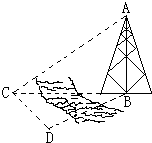如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C与D，测得∠BCD=75°，∠BDC=60°，CD=40（米），并在点C测得塔顶A的仰角为30°．则塔高AB=函数y=tan（2x+
）的定义域为（ ）
| π |
| 4 |
A、{x|x≠
| ||||
B、{x|x≠kπ+
| ||||
C、{x|x≠
| ||||
D、{x|x≠kπ-
|