题目内容
已知数列{an}满足an=an+1+2an•an+1,且a1=1.
(1)证明{
}是等差数列;
(2)令bn=an•an+1,求{bn}的前n项的和Sn.
(1)证明{
| 1 |
| an |
(2)令bn=an•an+1,求{bn}的前n项的和Sn.
考点:数列的求和,等差关系的确定
专题:等差数列与等比数列
分析:(1)由数列{an}满足an=an+1+2an•an+1,且a1=1.变形为
-
=2,即可证明.
(2)由(1)可得:
=2n-1,an=
.于是bn=an•an+1=
=
(
-
).利用“裂项求和”即可得出.
| 1 |
| an+1 |
| 1 |
| an |
(2)由(1)可得:
| 1 |
| an |
| 1 |
| 2n-1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
证明:(1)∵数列{an}满足an=an+1+2an•an+1,且a1=1.
∴
-
=2,
∴{
}是等差数列,首项为
=1;
(2)解:由(1)可得:
=1+2(n-1)=2n-1,∴an=
.
∴bn=an•an+1=
=
(
-
).
∴{bn}的前n项的和Sn=
[(1-
)+(
-
)+…+(
-
)]
=
(1-
)
=
.
∴
| 1 |
| an+1 |
| 1 |
| an |
∴{
| 1 |
| an |
| 1 |
| a1 |
(2)解:由(1)可得:
| 1 |
| an |
| 1 |
| 2n-1 |
∴bn=an•an+1=
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴{bn}的前n项的和Sn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
=
| n |
| 2n+1 |
点评:本题考查了等差数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=2x-3的零点所在的区间是( )
| A、(3,4) |
| B、(2,3) |
| C、(1,2) |
| D、(0,1) |
执行如图所示的程序框图,则输出的结果为( )


| A、20 | B、30 | C、35 | D、40 |
曲线y=x2上的点P处的切线的倾斜角为
,则点P的坐标为( )
| π |
| 4 |
| A、(0,0) | ||||
| B、(2,4) | ||||
C、(
| ||||
D、(
|
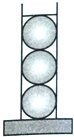 圆柱形容器内盛有高度为12cm的水,若放入三个不同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是
圆柱形容器内盛有高度为12cm的水,若放入三个不同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是