题目内容
设f(x)为定义在R上的奇函数,当x≥0时,f(x)=log3(2x+1),则f(-4)= .
考点:函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:运用奇函数的定义得f(-x)=-f(x),再由已知解析式,求出f(4),即可得到所求值.
解答:
解:由于f(x)为定义在R上的奇函数,
则f(-x)=-f(x),
当x≥0时,f(x)=log3(2x+1),
则f(4)=log3(8+1)=2,
则f(-4)=-f(4)=-2.
故答案为:-2.
则f(-x)=-f(x),
当x≥0时,f(x)=log3(2x+1),
则f(4)=log3(8+1)=2,
则f(-4)=-f(4)=-2.
故答案为:-2.
点评:本题考查函数的奇偶性的运用:求函数值,注意运用定义和已知解析式,考查运算能力,属于基础题.

练习册系列答案
相关题目
某种商品自投放市场以来,经过两次涨价,单价由原来的1280元涨到2000元,则这种商品平均每次涨价的百分率是( )
| A、28% | B、25% |
| C、20% | D、16% |
log336-log34=( )
| A、2 | ||
| B、0 | ||
C、
| ||
| D、-2 |
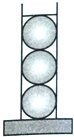 圆柱形容器内盛有高度为12cm的水,若放入三个不同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是
圆柱形容器内盛有高度为12cm的水,若放入三个不同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是