题目内容
不等式x2+2x＜
+
对任意a，b∈（0，+∞）恒成立，则实数x的取值范围是（ ）
| a |
| b |
| 16b |
| a |
| A、hmax（x） |
| B、（-∞，-2）∪（0，+∞） |
| C、（-4，2） |
| D、（-∞，-4）∪（2，+∞） |
考点：基本不等式,二次函数的性质
专题：不等式的解法及应用
分析：a，b＞0，利用基本不等式的性质可得
+
的最小值，由于不等式x2+2x＜
+
对任意a，b∈（0，+∞）恒成立?不等式x2+2x＜(
+
)min，a，b＞0．即可得出．
| a |
| b |
| 16b |
| a |
| a |
| b |
| 16b |
| a |
| a |
| b |
| 16b |
| a |
解答：
解：∵a，b＞0，∴
+
≥2
=8，当且仅当a=4b＞0时取等号．
∵不等式x2+2x＜
+
对任意a，b∈（0，+∞）恒成立?不等式x2+2x＜(
+
)min，a，b＞0．
∴x2+2x＜8，解得-4＜x＜2．
∴实数x的取值范围是（-4，2）．
故选：C．
| a |
| b |
| 16b |
| a |
|
∵不等式x2+2x＜
| a |
| b |
| 16b |
| a |
| a |
| b |
| 16b |
| a |
∴x2+2x＜8，解得-4＜x＜2．
∴实数x的取值范围是（-4，2）．
故选：C．
点评：本题考查了基本不等式的性质、恒成立问题的等价转化方法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
已知周期为4的函数f（x）=
，其中m＞0，若关于x的方，3f（x）=x恰有5个不同实数解，则m的取值范围是（ ）
|
A、（
| ||||||
B、（
| ||||||
C、（
| ||||||
D、（
|
函数f（x）=2x-3的零点所在的区间是（ ）
| A、（3，4） |
| B、（2，3） |
| C、（1，2） |
| D、（0，1） |
给定下列4个命题
①常数列既是等差数列，又是等比数列；
②若x＞a2+b2，则x＞2ab；
③若
⊥
，则
•
=0；
④垂直于同一直线的两直线平行．
其中正确的是（ ）
①常数列既是等差数列，又是等比数列；
②若x＞a2+b2，则x＞2ab；
③若
| a |
| b |
| a |
| b |
④垂直于同一直线的两直线平行．
其中正确的是（ ）
| A、①和② | B、②和④ |
| C、②和③ | D、①和④ |
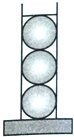圆柱形容器内盛有高度为12cm的水，若放入三个不同的球（球的半径与圆柱的底面半径相同）后，水恰好淹没最上面的球（如图所示），则球的半径是