题目内容
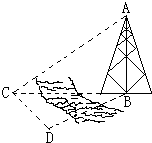 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=40(米),并在点C测得塔顶A的仰角为30°.则塔高AB=
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=40(米),并在点C测得塔顶A的仰角为30°.则塔高AB=考点:解三角形的实际应用
专题:解三角形
分析:由已知得∠CBD=45°,
=
,从而BC=20
,再由tan30°=
=
,能求出塔高AB.
| CD |
| sin∠CBD |
| BC |
| sin∠BDC |
| 6 |
| AB |
| BC |
| ||
| 3 |
解答:
解:因为∠BCD=75°,∠BDC=60°,
所以∠CBD=45°,
在△BCD中,根据正弦定理可知
=
,
即
=
,解得BC=20
,
在直角△ABC中,tan30°=
=
,
所以AB=
×20
=20
(米).
故答案为:20
.
所以∠CBD=45°,
在△BCD中,根据正弦定理可知
| CD |
| sin∠CBD |
| BC |
| sin∠BDC |
即
| 40 |
| sin45° |
| BC |
| sin60° |
| 6 |
在直角△ABC中,tan30°=
| AB |
| BC |
| ||
| 3 |
所以AB=
| ||
| 3 |
| 6 |
| 2 |
故答案为:20
| 2 |
点评:本题考查塔高的求法,是中档题,解题时要注意正弦定理的合理运用.

练习册系列答案
相关题目
已知log3(2x-1)<1,则的取值范围为( )
| A、x<2 | ||
| B、x>2 | ||
C、
| ||
| D、0<x<2 |
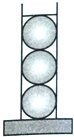 圆柱形容器内盛有高度为12cm的水,若放入三个不同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是
圆柱形容器内盛有高度为12cm的水,若放入三个不同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是