题目内容
已知
,则2x2-3y的最大值为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z的几何意义,利用数形结合即可得到结论.
解答:
解:作出不等式组对应的平面区域如图:
设z=2x2-3y,
则y=
x2-
,
由图象可知当抛物线经过点B时,抛物线取得最小值,
此时z最大,
由
,
解得
,即B(2,1),
此时z=2×22-3=5,
故答案为:5
设z=2x2-3y,

则y=
| 2 |
| 3 |
| z |
| 3 |
由图象可知当抛物线经过点B时,抛物线取得最小值,
此时z最大,
由
|
解得
|
此时z=2×22-3=5,
故答案为:5
点评:本题主要考查线性规划的应用,结合抛物线以及利用数形结合是解决本题的关键.

练习册系列答案
相关题目
给定下列4个命题
①常数列既是等差数列,又是等比数列;
②若x>a2+b2,则x>2ab;
③若
⊥
,则
•
=0;
④垂直于同一直线的两直线平行.
其中正确的是( )
①常数列既是等差数列,又是等比数列;
②若x>a2+b2,则x>2ab;
③若
| a |
| b |
| a |
| b |
④垂直于同一直线的两直线平行.
其中正确的是( )
| A、①和② | B、②和④ |
| C、②和③ | D、①和④ |
已知log3(2x-1)<1,则的取值范围为( )
| A、x<2 | ||
| B、x>2 | ||
C、
| ||
| D、0<x<2 |
某种商品自投放市场以来,经过两次涨价,单价由原来的1280元涨到2000元,则这种商品平均每次涨价的百分率是( )
| A、28% | B、25% |
| C、20% | D、16% |
log336-log34=( )
| A、2 | ||
| B、0 | ||
C、
| ||
| D、-2 |
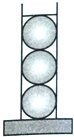 圆柱形容器内盛有高度为12cm的水,若放入三个不同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是
圆柱形容器内盛有高度为12cm的水,若放入三个不同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是