题目内容
函数y=tan(2x+
)的定义域为( )
| π |
| 4 |
A、{x|x≠
| ||||
B、{x|x≠kπ+
| ||||
C、{x|x≠
| ||||
D、{x|x≠kπ-
|
考点:正切函数的定义域
专题:函数的性质及应用
分析:直接由2x+
的终边不在y轴上求解x的取值集合得答案.
| π |
| 4 |
解答:
解:由2x+
≠kπ+
,得2x≠kπ+
,
∴x≠
+
,k∈Z.
∴函数y=tan(2x+
)的定义域为{x|x≠
+
,k∈Z}.
故选:A.
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
∴x≠
| kπ |
| 2 |
| π |
| 8 |
∴函数y=tan(2x+
| π |
| 4 |
| kπ |
| 2 |
| π |
| 8 |
故选:A.
点评:本题考查了与正切函数有关的复合函数单调性的求法,是基础题.

练习册系列答案
相关题目
已知log3(2x-1)<1,则的取值范围为( )
| A、x<2 | ||
| B、x>2 | ||
C、
| ||
| D、0<x<2 |
某种商品自投放市场以来,经过两次涨价,单价由原来的1280元涨到2000元,则这种商品平均每次涨价的百分率是( )
| A、28% | B、25% |
| C、20% | D、16% |
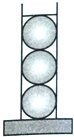 圆柱形容器内盛有高度为12cm的水,若放入三个不同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是
圆柱形容器内盛有高度为12cm的水,若放入三个不同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是