题目内容
过点A（23，2）作圆（x+1）2+（y-2）2=625的弦，其中弦长为整数的条数为（ ）
| A、36 | B、37 | C、72 | D、74 |
考点：直线与圆相交的性质
专题：直线与圆
分析：由圆的方程找出圆心B坐标及半径r的值，判断得到A在圆B内，得到过A最长的弦为直径MN，最短的弦为与直径MN垂直的弦CD，求出AB与CD的长，即可确定出弦长为整数的条数．
解答：
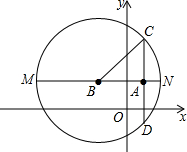解：由圆的方程得到圆心B（-1，2），半径r=25，
∵|AB|=
=24＜25，
∴点A在圆B内，
过A最长的弦为直径MN，最短的弦为与直径MN垂直的弦CD，
连接BC，
在Rt△ABC中，|BC|=25，|AB|=24，
根据勾股定理得：AC=
=7，
∴CD=2AC=14，
∴过A弦长的范围为14≤x≤50，
根据对称性，每个长度对应两条弦，
则弦长为整数的条数为35×2+2=72条，
故选C．
解：由圆的方程得到圆心B（-1，2），半径r=25，∵|AB|=
| (-1-23)2+(2-2)2 |
∴点A在圆B内，
过A最长的弦为直径MN，最短的弦为与直径MN垂直的弦CD，
连接BC，
在Rt△ABC中，|BC|=25，|AB|=24，
根据勾股定理得：AC=
| BC2-AB2 |
∴CD=2AC=14，
∴过A弦长的范围为14≤x≤50，
根据对称性，每个长度对应两条弦，
则弦长为整数的条数为35×2+2=72条，
故选C．
点评：此题考查了直线与圆相交的性质，涉及的知识有：垂径定理，勾股定理，根据题意得出“过A最长的弦为直径MN，最短的弦为与直径MN垂直的弦CD”是解本题的关键．
练习册系列答案
相关题目
执行如图的程序框图输出的T的值为（ ）
| A、4 | B、6 | C、8 | D、10 |
复数z=
在复平面上所对应的点Z位于（ ）
| (i+1)(i-1) |
| i |
| A、实轴上 | B、虚轴上 |
| C、第一象限 | D、第二象限 |
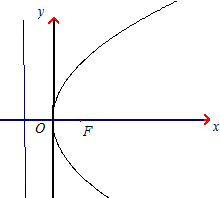已知抛物线y2=2px（p＞0），其焦点为F，一条过焦点F，倾斜角为θ（0＜θ＜π）的直线交抛物线于A，B两点，连接AO（O为坐标原点），交准线于点B'，连接BO，交准线于点A'，求四边形ABB'A'的面积．