题目内容

复数z=
(i+1)(i-1)
i
在复平面上所对应的点Z位于（　　）
A、实轴上B、虚轴上
C、第一象限D、第二象限
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：根据复数的几何意义，将复数进行化简即可．
解答： 解：z=
(i+1)(i-1)
i
=
i2-1
i
=
-2
i
=-2i，故对应的点的坐标为（0，-2），
在虚轴上，
故选：B
点评：本题主要考查复数的基本运算，利用复数的几何意义是解决本题的关键，比较基础．
练习册系列答案
相关题目
运行如图所示的程序框图，当输入实数x的值为-1时，输出的函数值为2；当输入实数x的值为3时，输出的函数值为7．
（Ⅰ）求实数a，b的值；并写出函数f（x）的解析式；
（Ⅱ）求满足不等式f（x）＞1的x的取值范围．
已知|
OA
|=1，|
OB
|=2，∠AOB=
2π
3
，
OC
=
1
2
OA
+
1
4
OB
，则
OA
与
OC
的夹角大小为
 
．
在如图所示的程序框图中，输入f0（x）=cosx，则输出的是（　　）
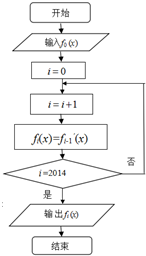
A、sinxB、-sinx
C、cosxD、-cosx
过点A（23，2）作圆（x+1）2+（y-2）2=625的弦，其中弦长为整数的条数为（　　）
A、36B、37C、72D、74
集合A={x|2≤x＜4}，B={x|x≥3}，则A∩B=（　　）
A、[2，4）
B、[3，+∞）
C、[3，4）
D、[2，3）
设抛物线C的方程为：y2=2px（p＞0），焦点为F，过点F作直线交抛物线C于A、B两点，且
AF
=2
F B

（1）若设直线AB的方程为x=ay+
p
2
的形式，求a2的值；
（2）若线段AB的中点到抛物线的准线的距离为
9
4
，求C的方程；
（3）设P（x0，y0）（x0＞2）是（2）中所求抛物线C上的动点，定点Q（2，0），线段PQ的垂直平分线与x轴交于点M（m，0），求实数m的最小值．
对于数列{an}，把a1作为新数列{bn}的第一项，把ai或-ai（i=2，3，4，…，n）作为新数列{bn}的第i项，数列{bn}称为数列{an}的一个生成数列．例如，数列1，2，3，4，5的一个生成数列是1，-2，-3，4，5．已知数列{bn}为数列{
1
2n
}（n∈N*）的生成数列，Sn为数列{bn}的前n项和．
（Ⅰ）写出S3的所有可能值；
（Ⅱ）若生成数列{bn}满足S3n=
1
7
（1-
1
8n
），求数列{bn}的通项公式；
（Ⅲ）证明：对于给定的n∈N*，Sn的所有可能值组成的集合为{x|x=
2k-1
2n
，k∈N*，k≤2n-1}．
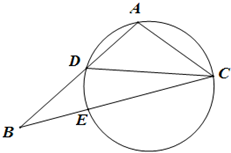如图，在△ABC中，CD是∠ACB的平分线，△ACD的外接圆交BC于点E，AC=2，AB=3，EC=
5
2
，则AD的长为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网