题目内容
设ave{a,b,c}表示实数a,b,c的平均数,max{a,b,c}表示实数a,b,c的最大值.设A=ave{-
x+2,x,
x+1},M=max{-
x+2,x,
x+1},若M=3|A-1|,则x的取值范围是 .
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
考点:函数的最值及其几何意义
专题:分类讨论
分析:由已知中max{a,b,c}表示a,b,c三个实数中的最大数,若M=3|A-1|=|x|,M是一个分段函数,所以要对x的取值进行讨论,从而求出满足条件的x范围.
解答:
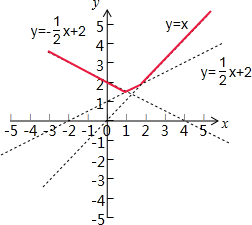 解:由题意易得A=
解:由题意易得A=
x+1,故3|A-1|=|x|=
,
∵M=3|A-1|,
∴当x<0时,-x=-
x+2,得x=-4;
当0≤x<1时,x=-
x+2,得x=
,舍去;
当1≤x<2时,x=
x+1,得x=2,舍去;
当x≥2时,x=x,恒成立,
综上所述,x=-4或x≥2.
故答案为:{x|x=-4或x≥2}.
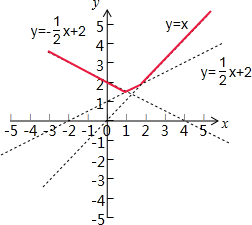 解:由题意易得A=
解:由题意易得A=| 1 |
| 3 |
|
∵M=3|A-1|,
∴当x<0时,-x=-
| 1 |
| 2 |
当0≤x<1时,x=-
| 1 |
| 2 |
| 4 |
| 3 |
当1≤x<2时,x=
| 1 |
| 2 |
当x≥2时,x=x,恒成立,
综上所述,x=-4或x≥2.
故答案为:{x|x=-4或x≥2}.
点评:点评:本题考查的知识点是分段函数的最值,运用了分类讨论思想和数形结合思想,结合函数的图象会更好理解.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
阅读如图程序框图,输出的结果i的值为( )
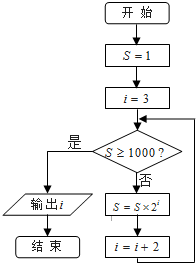

| A、5 | B、6 | C、7 | D、9 |
在如图所示的程序框图中,输入f0(x)=cosx,则输出的是( )
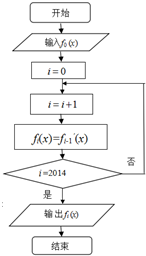

| A、sinx | B、-sinx |
| C、cosx | D、-cosx |
过点A(23,2)作圆(x+1)2+(y-2)2=625的弦,其中弦长为整数的条数为( )
| A、36 | B、37 | C、72 | D、74 |