题目内容
等边三角形ABC的边长为3,点D、E分别是边AB、AC上的点,且满足
=
=
(如图1).将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B成直二面角,连结A1B、A1C(如图1).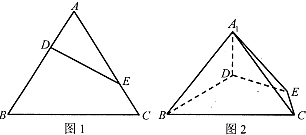
(Ⅰ)求证:A1D⊥平面BCED:
(Ⅱ)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角的正弦值为
?若存在,求出PB的长,若不存在,请说明理由.
| AD |
| DB |
| CE |
| EA |
| 1 |
| 2 |

(Ⅰ)求证:A1D⊥平面BCED:
(Ⅱ)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角的正弦值为
| ||
| 2 |
考点:直线与平面所成的角,平面与平面垂直的判定
专题:空间角
分析:(Ⅰ)由已知条件推导出AD=1,AE=2,DE=
,从而得到AD⊥DE,拆叠后有A1D⊥DE,由此能够证明A1D⊥平面BCED.
(Ⅱ)假设在线段BC上存在点P,使直线PA1与平面A1BD所成的角的正弦值为
.作PH⊥BD于点H,连结A1H,A1P,由已知条件推导出∠PA1H是直线PA1与平面A1BD所成的角,且∠PA1H=60°,由此能推导出在线段BC上存在点P,使直线PA1与平面A1BD所成的角的正弦值为
,并能求出此时PB的长.
| 3 |
(Ⅱ)假设在线段BC上存在点P,使直线PA1与平面A1BD所成的角的正弦值为
| ||
| 2 |
| ||
| 2 |
解答:
(Ⅰ)证明:∵等边△ABC的边长为3,且
=
=
,
∴AD=1,AE=2,
在△ADE中,∠DAE=60°,
由余弦定理得DE=
=
,
∵AD2+DE2=AE2,
∴AD⊥DE,
拆叠后有A1D⊥DE,
∵二面角A1-DE-B是直二面角,
∴平面A1DE⊥平面BCED,
又∵平面A1DE∩平面BCED=DE,A1D?平面A1DE,A1D⊥DE,
∴A1D⊥平面BCED.
(Ⅱ)解:假设在线段BC上存在点P,
使直线PA1与平面A1BD所成的角的正弦值为
,
如图,作PH⊥BD于点H,连结A1H,A1P,
由(Ⅰ)有A1D⊥平面BCDE,
∵PH?平面BCED,∴A1D⊥PH,
又∵A1D∩BD=D,∴PH⊥平面A1BD,
∴∠PA1H是直线PA1与平面A1BD所成的角,
∵直线PA1与平面A1BD所成的角的正弦值为
,
∴∠PA1H=60°,
设PB=x(0≤x≤3),则BH=
,PH=
x,
在Rt△PA1H中,∠PA1H=60°,∴A1H=
x,
在Rt△A1DH中,A1D=1,DH=2-
x,
由A1D2+DH2=A1H2,
得12+(2-
x)2=(
x)2,解得x=
,满足0≤x≤3,符合题意,
∴在线段BC上存在点P,使直线PA1与平面A1BD所成的角的正弦值为
,
此时PB=
.
| AD |
| DB |
| CE |
| EA |
| 1 |
| 2 |
∴AD=1,AE=2,
在△ADE中,∠DAE=60°,
由余弦定理得DE=
| 12+22-2×1×2×cos60° |
| 3 |
∵AD2+DE2=AE2,
∴AD⊥DE,
拆叠后有A1D⊥DE,
∵二面角A1-DE-B是直二面角,

∴平面A1DE⊥平面BCED,
又∵平面A1DE∩平面BCED=DE,A1D?平面A1DE,A1D⊥DE,
∴A1D⊥平面BCED.
(Ⅱ)解:假设在线段BC上存在点P,
使直线PA1与平面A1BD所成的角的正弦值为
| ||
| 2 |
如图,作PH⊥BD于点H,连结A1H,A1P,
由(Ⅰ)有A1D⊥平面BCDE,
∵PH?平面BCED,∴A1D⊥PH,
又∵A1D∩BD=D,∴PH⊥平面A1BD,
∴∠PA1H是直线PA1与平面A1BD所成的角,
∵直线PA1与平面A1BD所成的角的正弦值为
| ||
| 2 |
∴∠PA1H=60°,
设PB=x(0≤x≤3),则BH=
| x |
| 2 |
| ||
| 2 |
在Rt△PA1H中,∠PA1H=60°,∴A1H=
| 1 |
| 2 |
在Rt△A1DH中,A1D=1,DH=2-
| 1 |
| 2 |
由A1D2+DH2=A1H2,
得12+(2-
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴在线段BC上存在点P,使直线PA1与平面A1BD所成的角的正弦值为
| ||
| 2 |
此时PB=
| 5 |
| 2 |
点评:本题考查直线与平面垂直的证明,考查满足条件的点是否存在的判断,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则如图所示,例如明文1,2,3,4,对应密文5,7,18,16.当对方收到密文14,9,23,28时,则解密得到的明文为( )
为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则如图所示,例如明文1,2,3,4,对应密文5,7,18,16.当对方收到密文14,9,23,28时,则解密得到的明文为( )| A、4,6,1,7 |
| B、6,4,1,7 |
| C、1,6,4,7 |
| D、7,6,1,4 |
阅读如图程序框图,输出的结果i的值为( )
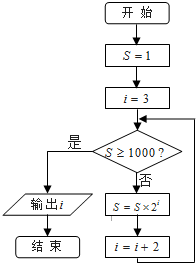

| A、5 | B、6 | C、7 | D、9 |
过点A(23,2)作圆(x+1)2+(y-2)2=625的弦,其中弦长为整数的条数为( )
| A、36 | B、37 | C、72 | D、74 |
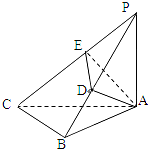 如图,已知PA⊥平面ABC,等腰直角三角形ABC中,AB=BC=2,AB⊥BC,AD⊥PB于D,AE⊥PC于E.
如图,已知PA⊥平面ABC,等腰直角三角形ABC中,AB=BC=2,AB⊥BC,AD⊥PB于D,AE⊥PC于E. 运行如图所示的程序框图,当输入实数x的值为-1时,输出的函数值为2;当输入实数x的值为3时,输出的函数值为7.
运行如图所示的程序框图,当输入实数x的值为-1时,输出的函数值为2;当输入实数x的值为3时,输出的函数值为7.