题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为e=
,以原点为圆心,椭圆短半轴长为半径的圆与直线x-y+
=0相切.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设F1(-1,0),F2(1,0),若过F1的直线交曲线C于A、B两点,求
•
的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设F1(-1,0),F2(1,0),若过F1的直线交曲线C于A、B两点,求
| F2A |
| F2B |
考点:直线与圆锥曲线的综合问题
专题:向量与圆锥曲线
分析:(Ⅰ)由直线到圆的距离计算出b,再写出标准方程;
(Ⅱ)①当AB斜率为0时,计算
•
的值,
②当AB的斜率不为0时,设出AB的方程为:x+1=my,联立方程组,求出
•
的表达式,再计算其范围.
(Ⅱ)①当AB斜率为0时,计算
| F2A |
| F2B |
②当AB的斜率不为0时,设出AB的方程为:x+1=my,联立方程组,求出
| F2A |
| F2B |
解答:
解:(Ⅰ)由题意可得圆的方程为x2+y2=b2,
∵直线x-y+
=0与圆相切,∴d=
=b,即b=1,
又e=
=
,及a2=b2+c2,得a=2,所以椭圆方程为
+y2=1.
(Ⅱ)①当直线AB的斜率为0时,A(-
,0),B(
,0)时,
•
=-1
②当直线AB的斜率不为0时,不妨设AB的方程为:x+1=my
由
得:(m2+2)y2-2my-1=0,
设A(x1,y1),B(x2,y2)则:y1+y2=
,y1y2=-
,
∴
•
=(x1-1,y1)•(x2-1,y2)=(my1-2,y1)•(my2-2,y2)
=(my1-2)(my2-2)+y1y2=(m2+1)y1y2-2m(y1+y2)+4
=-
-2m•
+4=
+4
=-1+
∈(-1,
],
由①、②得:
•
的取值范围为[-1,
].
∵直线x-y+
| 2 |
| ||
|
又e=
| c |
| a |
| ||
| 2 |
| x2 |
| 2 |
(Ⅱ)①当直线AB的斜率为0时,A(-
| 2 |
| 2 |
| F2A |
| F2B |
②当直线AB的斜率不为0时,不妨设AB的方程为:x+1=my
由
|
设A(x1,y1),B(x2,y2)则:y1+y2=
| 2m |
| m2+2 |
| 1 |
| m2+2 |
∴
| F2A |
| F2B |
=(my1-2)(my2-2)+y1y2=(m2+1)y1y2-2m(y1+y2)+4
=-
| m2+1 |
| m2+2 |
| 2m |
| m2+2 |
| -5m2-1 |
| m2+2 |
=-1+
| 9 |
| m2+2 |
| 7 |
| 2 |
由①、②得:
| F2A |
| F2B |
| 7 |
| 2 |
点评:本题是圆锥曲线和向量知识的综合,是高考中的常见考点,本题中设而不求得数学方法也是圆锥曲线中最常见的解题方法,计算时不要忘了分两种情况讨论.另外,本题也给我们提供了一种解决圆锥曲线问题的思路--向量的方法.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
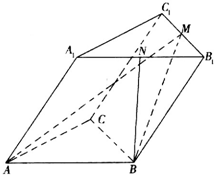 如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是B1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°.
如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是B1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°.