题目内容
在平面直角坐标系xOy中,已知椭圆C:
+
=1(a>b>0)的焦距为2,且点(
,
)在椭圆C上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点A,B分别是椭圆C的左右顶点,直线经过点B且垂直于x轴,点P是椭圆C上异于点A,B的任意一点,直线AP交于点M,设直线OM,PB的斜率分别为k1,k2,求证:k1•k2为定值.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点A,B分别是椭圆C的左右顶点,直线经过点B且垂直于x轴,点P是椭圆C上异于点A,B的任意一点,直线AP交于点M,设直线OM,PB的斜率分别为k1,k2,求证:k1•k2为定值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用椭圆C的焦距为2,可得a2-b2=1,根据点(
,
)在椭圆C上,求出参数a,b,即可求出椭圆C的方程;
(Ⅱ)证明:法1:由条件可得直线PB的方程,代入椭圆方程,求出P的坐标,可得PA的方程,令x=2,得y=-
,即M(2,-
),即可证明结论;法2:利用斜率的计算公式、三点共线的斜率性质、点在椭圆上的性质即可证明;
| 2 |
| ||
| 2 |
(Ⅱ)证明:法1:由条件可得直线PB的方程,代入椭圆方程,求出P的坐标,可得PA的方程,令x=2,得y=-
| 3 |
| k2 |
| 3 |
| k2 |
解答:
(Ⅰ)解:∵椭圆C的焦距为2,
∴c=1,∴a2-b2=1①--(2分)
又点(
,
)在椭圆C上⇒
+
=1②--(4分)
联立①②得a2=4,b2=3,或a2=
<1(会去)
故椭圆C的方程:
+
=1.--(6分)
(Ⅱ)证明:法1:由条件可得直线PB的方程为:y=k2(x-2),设P(xP,yP).
由
,得(3+4k22)x2-16k22x+16k22-12=0(*)--(8分)
易知xP,2为(*)方程的两根,则2xP=
,
∴xP=
,yP=
,
则kPA=
=-
.--(10分)
故直线PA的方程为:y=-
(x+2).
令x=2,得y=-
,即M(2,-
),则k1=
=-
,∴k1k2=-
.--(12分)
法2:P(xP,yP)(xp≠±2),M(2,yM),则k2=
,且
+
=1.
又A,P,M三点共线,则
∥
.
∵
=(xP+2,yP),
=(4,yM),
∴4yP=yM(xP+2)⇒yM=
.
则k1=
,∴k1k2=
=
=-
.
∴c=1,∴a2-b2=1①--(2分)
又点(
| 2 |
| ||
| 2 |
| 2 |
| a2 |
| 3 |
| 2b2 |
联立①②得a2=4,b2=3,或a2=
| 1 |
| 2 |
故椭圆C的方程:
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)证明:法1:由条件可得直线PB的方程为:y=k2(x-2),设P(xP,yP).
由
|
易知xP,2为(*)方程的两根,则2xP=
16
| ||
3+4
|
∴xP=
8
| ||
3+4
|
| -12k2 | ||
3+4
|
则kPA=
| ||||||
|
| 3 |
| 4k2 |
故直线PA的方程为:y=-
| 3 |
| 4k2 |
令x=2,得y=-
| 3 |
| k2 |
| 3 |
| k2 |
-
| ||
| 2 |
| 3 |
| 2k2 |
| 3 |
| 2 |
法2:P(xP,yP)(xp≠±2),M(2,yM),则k2=
| yP |
| xP-2 |
| xP2 |
| 4 |
| yP2 |
| 3 |
又A,P,M三点共线,则
| AP |
| AM |
∵
| AP |
| AM |
∴4yP=yM(xP+2)⇒yM=
| 4y P |
| xP+2 |
则k1=
| 2yP |
| xp+2 |
| 2yP |
| xP2-4 |
6(1-
| ||
| xP2-4 |
| 3 |
| 2 |
点评:熟练掌握椭圆的定义及其性质、斜率的计算公式及其直线的点斜式是解题的关键.善于利用已经证明过的结论是解题的技巧.

练习册系列答案
相关题目
下列说法正确的是( )
| A、当直线l1与l2的斜率k1,k2满足k1•k2=-1时,两直线一定垂直 | ||||
B、直线Ax+By+C=0的斜率为-
| ||||
C、过(x1,y1),(x2,y2)两点的所有直线的方程
| ||||
| D、经过点(1,1)且在x轴和y轴上截距都相等的直线方程为x+y-2=0 |
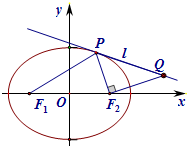 在平面直角坐标系xoy中,已知F1,F2分别是椭圆G:
在平面直角坐标系xoy中,已知F1,F2分别是椭圆G: 如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为2,则∠BDF的余弦值是
如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为2,则∠BDF的余弦值是