题目内容
12．已知An4=24Cn6，且（1-2x）n=a0+a1x+a2x2+a3x3+…+anxn．（1）求n的值；
（2）求a1+a2+a3+…+an的值．
分析 （1）由条件利用排列数、组合数的计算公式，求得n的值．
（2）在所给的二项式中，令x=0求得a0=1，再令x=1，可得 a0+a1+a2+a3+…+an的值，从而求得x=1，可得a1+a2+a3+…+an的值．
解答 解：（1）由An4=24Cn6，可得$\frac{n!}{（n-4）!}$=24•$\frac{n!}{（n-6）!•6!}$，（n-4）（n-5）=5×6，
求得n=10或n=-1（舍去），故n=10．
（2）在（1-2x）n=a0+a1x+a2x2+a3x3+…+anxn中，
令x=0，可得a0=1；
再令x=1，可得 a0+a1+a2+a3+…+an=a0+a1+a2+a3+…+a10=1，
∴a1+a2+a3+…+an的=a1+a2+a3+…+a10=0．
点评 本题主要考查排列数、组合数的计算公式，二项式定理的应用，属于给变量赋值问题，属于基础题．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
2．已知O为坐标原点，A，B为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个顶点，点P是双曲线上异于A，B的一点，连接PO交椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1于点Q，设直线PA，PB，QA，QB的斜率分别为k1，k2，k3，k4，则k1+k2+k3+k4的值为（ ）
| A． | 0 | B． | -1 | C． | $\frac{1}{2}$ | D． | 1 |
20．“a=-2”是“直线ax+2y=0垂直于直线x+y=1”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 既不充分也不必要条件 | D． | 充要条件 |
7．
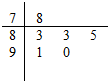对某同学的6次数学测试成绩（满分100分）进行统计，作出的茎叶如图所示，给出关于该同学数学成绩的以下说法：
①中位数为83；②众数为83；③平均数为85；④极差为12．
其中正确说法序号是（ ）
对某同学的6次数学测试成绩（满分100分）进行统计，作出的茎叶如图所示，给出关于该同学数学成绩的以下说法：①中位数为83；②众数为83；③平均数为85；④极差为12．
其中正确说法序号是（ ）
| A． | ①② | B． | ③④ | C． | ②③ | D． | ①③ |
4．设直线y=3x-2与椭圆Г：$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1交于A，B两点，过A，B两点的圆与椭圆Г交于另外两点C，D，则直线CD的斜率k为（ ）
| A． | -$\frac{1}{3}$ | B． | -3 | C． | $\frac{1}{2}$ | D． | -2 |