题目内容
4.设直线y=3x-2与椭圆Г:$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1交于A,B两点,过A,B两点的圆与椭圆Г交于另外两点C,D,则直线CD的斜率k为( )| A. | -$\frac{1}{3}$ | B. | -3 | C. | $\frac{1}{2}$ | D. | -2 |
分析 过A,B两点的圆与椭圆Г交于另外两点C,D,运用曲线系方程,令参数为0,即可得到所求斜率.
解答 解:由直线AB:y=3x-2,可得斜率为3,
再由过A,B两点的圆与椭圆Г交于另外两点C,D,
由y=3x-2可得y2-(3x-2)2=0,
过直线AB,直线CD和椭圆的曲线系方程为
y2-(3x-2)2+λ(16x2+25y2-400)=0,
可得(1+25λ)y2+(16λ-9)x2+12x-4-400λ=0,
由1+25λ=16λ-9,解得λ=-$\frac{10}{9}$,
可得λ=-$\frac{10}{9}$表示圆的方程,
求交点弦方程,可运用曲线系方程的结论,可令λ=0,即有y2=(3x-2)2,
即为y=3x-2和y=-3x+2,
即有k=-3.
故选:B.
点评 本题考查直线和圆、椭圆的位置关系,考查圆与椭圆的位置关系的判断,注意运用曲线系方程解题,属于中档题.

练习册系列答案
相关题目
9.函数y=2sin(ωx+φ)的部分图象如图所示,则ω,φ可以取的一组值是( )
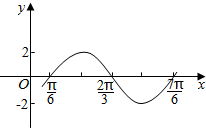

| A. | ω=2,φ=-$\frac{π}{3}$ | B. | ω=2,φ=$\frac{π}{3}$ | C. | ω=2,ω=-$\frac{π}{6}$ | D. | ω=1,φ=$\frac{π}{6}$ |
13.已知两条直线:y=(a-1)x-2和3x+(a+3)y-1=0互相平行,则a等于 ( )
| A. | 0 或-2 | B. | -2 或-1 | C. | 1或-2 | D. | 0或2 |