题目内容
1.已知等比数列{an}的前n项和为Sn,a1=$\frac{1}{2}$,anan+1>0(n∈N*),S3+a3,S5+a5,S4+a4成等差数列.(1)求数列{an}的通项公式;
(1)设bn=nan,求数列{bn}的前n项和Tn.
分析 (1)通过S3+a3,S5+a5,S4+a4成等差数列可知S5+a5-(S3+a3)=S4+a4-(S5+a5),整理可知4a5=a3,通过设等比数列{an}的公比为q,利用q2=$\frac{{a}_{5}}{{a}_{3}}$及anan+1>0可知q=$\frac{1}{2}$,进而计算可得结论;
(2)通过(1)可知bn=n•$\frac{1}{{2}^{n}}$,进而利用错位相减法计算计算即得结论.
解答 解:(1)因为S3+a3,S5+a5,S4+a4成等差数列,
所以S5+a5-(S3+a3)=S4+a4-(S5+a5),
化简得4a5=a3,
设等比数列{an}的公比为q,则q2=$\frac{{a}_{5}}{{a}_{3}}$=$\frac{1}{4}$,
因为anan+1=${{a}_{1}}^{2}$•q2n-1>0,
所以q>0,从而q=$\frac{1}{2}$,
故数列{an}的通项公式an=$\frac{1}{{2}^{n}}$;
(2)由(1)可知bn=nan=n•$\frac{1}{{2}^{n}}$,
所以Tn=1•$\frac{1}{2}$+2•$\frac{1}{{2}^{2}}$+…+n•$\frac{1}{{2}^{n}}$,①
则$\frac{1}{2}$Tn=1•$\frac{1}{{2}^{2}}$+2•$\frac{1}{{2}^{3}}$+…+(n-1)•$\frac{1}{{2}^{n}}$+n•$\frac{1}{{2}^{n+1}}$,②
①-②,得$\frac{1}{2}$Tn=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$-n•$\frac{1}{{2}^{n+1}}$,
即Tn=1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n-1}}$-n•$\frac{1}{{2}^{n}}$
=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-n•$\frac{1}{{2}^{n}}$
=2-$\frac{n+2}{{2}^{n}}$.
点评 本题考查数列的通项及前n项和,考查错位相减法,注意解题方法的积累,属于中档题.

| A. | y=2|x| | B. | y=|log2x| | C. | y=x3 | D. | y=x-2 |
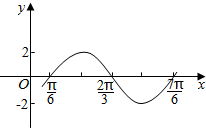
| A. | ω=2,φ=-$\frac{π}{3}$ | B. | ω=2,φ=$\frac{π}{3}$ | C. | ω=2,ω=-$\frac{π}{6}$ | D. | ω=1,φ=$\frac{π}{6}$ |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
| A. | 0 或-2 | B. | -2 或-1 | C. | 1或-2 | D. | 0或2 |
| A. | f(x)=1,f(x)=x0 | B. | f(x)=|x|,f(t)=$\sqrt{t^2}$ | ||
| C. | f(x)=$\frac{x^2-1}{x-1}$,g(x)=x+1 | D. | f(x)=$\sqrt{x+1}$•$\sqrt{x-1}$,g(x)=$\sqrt{x^2-1}$ |