题目内容
17.已知函数f(x)=$\frac{{4}^{x}}{{4}^{x}+2}$,则f($\frac{1}{2015}$)+f($\frac{2}{2015}$)+f($\frac{3}{2015}$)+…+f($\frac{2014}{2015}$)=1007.分析 由已知中函数f(x)=$\frac{{4}^{x}}{{4}^{x}+2}$,可得:f(x)+f(1-x)=1,进而得到答案.
解答 解:∵函数f(x)=$\frac{{4}^{x}}{{4}^{x}+2}$,
∴f(1-x)=$\frac{{4}^{1-x}}{{4}^{1-x}+2}$=$\frac{2}{{4}^{x}+2}$,
∴f(x)+f(1-x)=1,
∴f($\frac{1}{2015}$)+f($\frac{2}{2015}$)+f($\frac{3}{2015}$)+…+f($\frac{2014}{2015}$)=1007,
故答案为:1007.
点评 本题考查的知识点是函数求值,其中根据已知确定出f(x)+f(1-x)=1,是解答的关键.

练习册系列答案
相关题目
5.某单位有老年人27人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为42的样本,则老年人、中年人、青年人分别应抽取的人数是( )
| A. | 7,11,18 | B. | 6、12、18 | C. | 6、13、17 | D. | 7、14、21 |
2.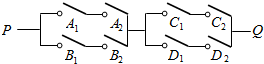 如图,在电路系统PQ中,用A1、A2、B1、B2、C1、C2、D1、D2表示8个开关,则使两端P、Q通电、不通电的开关闭合情况分别有(A)种、(D)种.
如图,在电路系统PQ中,用A1、A2、B1、B2、C1、C2、D1、D2表示8个开关,则使两端P、Q通电、不通电的开关闭合情况分别有(A)种、(D)种.
 如图,在电路系统PQ中,用A1、A2、B1、B2、C1、C2、D1、D2表示8个开关,则使两端P、Q通电、不通电的开关闭合情况分别有(A)种、(D)种.
如图,在电路系统PQ中,用A1、A2、B1、B2、C1、C2、D1、D2表示8个开关,则使两端P、Q通电、不通电的开关闭合情况分别有(A)种、(D)种.| A.49 | B.56 | C.200 | D.207 | E.360 | F.269. |
9.函数y=2sin(ωx+φ)的部分图象如图所示,则ω,φ可以取的一组值是( )
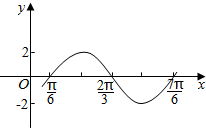

| A. | ω=2,φ=-$\frac{π}{3}$ | B. | ω=2,φ=$\frac{π}{3}$ | C. | ω=2,ω=-$\frac{π}{6}$ | D. | ω=1,φ=$\frac{π}{6}$ |
6.已知实数x、y满足$\left\{\begin{array}{l}{x-y-1≤0}\\{2x-y-3≥0}\end{array}\right.$,在区间(0,5)内任取两数a、b.则目标函数z=ax+by的最小值大于2$\sqrt{5}$的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |