题目内容
11.已知圆M的圆心在直线x+y=0上,半径为1,直线l:6x-8y-9=0被圆M截得的弦长为$\sqrt{3}$,且圆心M在直线l的右下方.(1)求圆M的标准方程;
(2)直线mx+y-m+1=0与圆M交于A,B两点,动点P满足|PO|=$\sqrt{2}$|PM|(O为坐标原点),试求△PAB面积的最大值,并求出此时P点的坐标.
分析 (1)利用直线l:6x-8y-9=0被圆M截得的弦长为$\sqrt{3}$,且圆心M在直线l的右下方,求出圆心坐标,即可求圆M的标准方程;
(2)要使△PAB的面积最大,点P到直线AB的距离d最大,利用P点在以(2,-2)为圆心,2为半径的圆上,即可得出结论.
解答 解:(1)由已知可设圆心M(a,-a),圆心到直线l的距离为d,
则d=$\frac{|6a+8a-9|}{10}$=$\sqrt{1-\frac{3}{4}}$,…(1分)
于是,整理得|14a-9|=5,解得a=1,或a=$\frac{2}{7}$.…(3分)
∵圆心M在直线l的右下方,
∴圆心M是(1,-1),
∴圆M的标准方程为(x-1)2+(y+1)2=1.…(4分)
(2)直线mx+y-m+1=0可变形为m(x-1)+y+1=0,即过定点(1,-1),
∴动直线mx+y-m+1=0恰好过圆M的圆心,
∴|AB|=2.…(5分)
设P(x,y),则由|PO|=$\sqrt{2}$|PM|,可得x2+y2=2[(x-1)2+(y+1)2],
整理得(x-2)2+(y+2)2=4,即P点在以(2,-2)为圆心,2为半径的圆上,…(7分)
设此圆圆心为N,则N(2,-2).
∴要使△PAB的面积最大,点P到直线AB的距离d最大,
dmax=|PM|=$\sqrt{(2-1)^{2}+(-2+1)^{2}}$+2=$\sqrt{2}$+2,
∴△PAB面积的最大值为=$\sqrt{2}+2$.…(8分)
∵MN的方程为y=-x,…(9分)
代入方程(x-2)2+(y+2)2=4中,可解得x=4,或0 (舍去),
∴此时P(4,-4).…(10分)
点评 本题考查圆的方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案| A. | m>2 | B. | 0<m<1 | C. | m>0 | D. | m>1 |
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
则这三天中恰有两天下雨的概率近似为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{15}$ | D. | $\frac{1}{5}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也必要条件 |
| A. | y=±$\sqrt{7}$x | B. | y=±7x | C. | y=±$\frac{\sqrt{7}}{7}$x | D. | y=±$\frac{1}{7}$x |
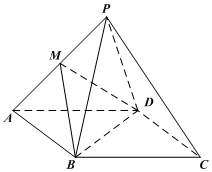 如图,在正四棱锥P-ABCD中,点M为侧棱PA的中点.
如图,在正四棱锥P-ABCD中,点M为侧棱PA的中点.