题目内容
对于函数f(x)=log
(x2-2ax+3),解答下述问题:
(1)若函数的定义域为R,求实数a的取值范围;
(2)若函数的值域为(-∞,-1],求实数a的值.
| 1 |
| 2 |
(1)若函数的定义域为R,求实数a的取值范围;
(2)若函数的值域为(-∞,-1],求实数a的值.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)若函数的定义域为R,则内函数u=g(x)=x2-2ax+3的最小值大于0,进而可得实数a的取值范围;
(2)函数的值域为(-∞,-1],则内函数u=g(x)=x2-2ax+3的最小值为2,进而可得实数a的值.
(2)函数的值域为(-∞,-1],则内函数u=g(x)=x2-2ax+3的最小值为2,进而可得实数a的值.
解答:
解:记u=g(x)=x2-2ax+3=(x-a)2+3-a2,
(1)∵u>0对x∈R恒成立,
∴umin=3-a2>0⇒-
<a<
,
∴a的取值范围是(-
,
);
(2)∵g(x)的值域是[3-a2,+∞),
∴函数的值域为(-∞,-1]等价于[g(x)]min=3-a2=2⇒a=±1;
即a的值为±1;
(1)∵u>0对x∈R恒成立,
∴umin=3-a2>0⇒-
| 3 |
| 3 |
∴a的取值范围是(-
| 3 |
| 3 |
(2)∵g(x)的值域是[3-a2,+∞),
∴函数的值域为(-∞,-1]等价于[g(x)]min=3-a2=2⇒a=±1;
即a的值为±1;
点评:本题考查的知识点是对数函数与性质,二次函数的图象和性质,是函数图象和性质的综合应用,难度中档.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知函数f(x)=ax3+bx2+x(a,b∈R且ab≠0)的图象如图,且|x1|>|x2|,则有( )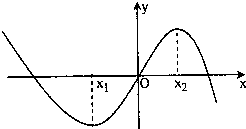

| A、a>0,b>0 |
| B、a<0,b<0 |
| C、a<0,b>0 |
| D、a>0,b<0 |
过抛物线的焦点F作互相垂直的两条直线,分别交准线于P、Q两点,又过P、Q分别作抛物线对称轴OF的平行线,交抛物线于M、N两点,则M、N、F三点( )
| A、共圆 | B、共线 |
| C、在另一抛物线上 | D、在一双曲线上 |
“k=±
”是“直线x-y+k=0与圆x2+y2=1相切”的( )
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也也必要条件 |