题目内容
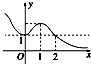
定义在R上的可导函数f（x），已知y=ef'（x）的图象如图所示，则y=f（x）的增区间是 ．
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：由题意知，欲求函数的增区间，由图象确定出函数导数为非负的区间就可以了，由于y=ef'（x）是一个指数型的函数，当指数大于0时函数值大于1，故由图象找出函数图象在直线y=1上面的那一部分的自变量的集合即为所求
解答：
解：由题意如图f'（x）≥0的区间是（-∞，2），
故函数y=f（x）的增区间（-∞，2），
故答案为：（-∞，2），
故函数y=f（x）的增区间（-∞，2），
故答案为：（-∞，2），
点评：本题考查函数的单调性与导数的关系，由于函数的导数是指数型函数的指数，故可以借助指数函数的图象观察出导数非负的区间，此即为函数的递增区间．
练习册系列答案
阅读快车系列答案
相关题目
某班有50名学生，在学校组织的一次数学质量抽测中，如果按照抽测成绩的分数段[60，65），[65，70），…[95，100）进行分组，得到的分布情况如图所示．求：