题目内容
已知向量
=（3，-1），
=（0，2），若
•
=0，
=λ
，则实数λ的值为 ．
| OA |
| OB |
| OC |
| AB |
| AC |
| OB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：设出
=（x，y），根据题意，求出
，再由
=λ
，求出λ的值．
| OC |
| OC |
| AC |
| OB |
解答：
解：设
=（x，y），
∵向量
=（3，-1），
=（0，2），
∴
=（x-3，y+1），
=（-3，3）；
又∵
•
=0，
∴-3x+3y=0①；
又∵
=λ
，
∴2（x-3）-0•（y+1）=0②；
由①、②组成方程组，
解得x=3，y=3；
∴（0，4）=λ（0，2），
∴λ=2．
故答案为：2．
| OC |
∵向量
| OA |
| OB |
∴
| AC |
| AB |
又∵
| OC |
| AB |
∴-3x+3y=0①；
又∵
| AC |
| OB |
∴2（x-3）-0•（y+1）=0②；
由①、②组成方程组，
解得x=3，y=3；
∴（0，4）=λ（0，2），
∴λ=2．
故答案为：2．
点评：本题考查了平面向量的数量积的应用问题，解题时应利用平面向量的数量积解答向量的垂直与平行问题，是基础题．
练习册系列答案
相关题目
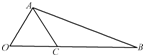如图，∠AOB=60°，OA=2，OB=5，在线段OB上任取一点C，试求：