题目内容
对于(2x-
)12的展开式,求:
(1)各项系数的和;
(2)奇数项系数的和;
(3)偶数项系数的和.
| 1 | ||
2
|
(1)各项系数的和;
(2)奇数项系数的和;
(3)偶数项系数的和.
考点:二项式定理的应用
专题:二项式定理
分析:在(2x-
)12的展开式中,令x=1,可得各项系数的和;在(2x+
)12的展开式中,令x=1,可得(2x-
)12的奇数项的系数和减去偶数项的系数的和;进而求得奇数项系数的和、偶数项系数的和.
| 1 | ||
2
|
| 1 | ||
2
|
| 1 | ||
2
|
解答:
解:(1)在(2x-
)12的展开式中,令x=1,可得各项系数的和为(
)12.
(2)、(3)在(2x+
)12的展开式中,令x=1,可得(2x-
)12的奇数项的系数和减去偶数项的系数的和为(
)12,
故(2x-
)12的奇数项的系数和为
,偶数项的系数的和为
.
| 1 | ||
2
|
| 3 |
| 2 |
(2)、(3)在(2x+
| 1 | ||
2
|
| 1 | ||
2
|
| 5 |
| 2 |
故(2x-
| 1 | ||
2
|
(
| ||||
| 2 |
(
| ||||
| 2 |
点评:本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 如图所示,为了测量某湖泊两侧A,B间的距离,李宁同学首先选定了与A,B不共线的一点C,然后给出了三种测量方案:(△ABC的角A,B,C所对的边分别记为a,b,c):①测量A,C,b;②测量a,b,C;③测量A,B,a.则一定能确定A,B间距离的所有方案的个数为( )
如图所示,为了测量某湖泊两侧A,B间的距离,李宁同学首先选定了与A,B不共线的一点C,然后给出了三种测量方案:(△ABC的角A,B,C所对的边分别记为a,b,c):①测量A,C,b;②测量a,b,C;③测量A,B,a.则一定能确定A,B间距离的所有方案的个数为( )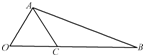 如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,试求:
如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,试求: