题目内容
设f(x)是定义在R上的奇函数,当x<0时,f′(x)>0,且f(-1)=0,则不等式f(x)<0的解集为 ( )
| A、{x|x<-1} |
| B、{x|0<x<1} |
| C、{x|x<-1或0<x<1} |
| D、{x|x≥1或-1<x<0} |
考点:函数的单调性与导数的关系,函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数奇偶性的性质,即可求解不等式.
解答:
解:∵f(x)是定义在R上的奇函数,f(-1)=0,
∴f(-1)=-f(1)=0,
即f(1)=0,
∵当x<0时,f′(x)>0,此时函数单调递增,
∴当x>0时,函数单调递增.
当x>0时,不等式f(x)<0的解为,0<x<1,
当x<0时,不等式f(x)<0的解为,x<-1
即不等式f(x)<0的解集为{x|x<-1或0<x<1},
故选:C.
∴f(-1)=-f(1)=0,
即f(1)=0,
∵当x<0时,f′(x)>0,此时函数单调递增,
∴当x>0时,函数单调递增.
当x>0时,不等式f(x)<0的解为,0<x<1,
当x<0时,不等式f(x)<0的解为,x<-1
即不等式f(x)<0的解集为{x|x<-1或0<x<1},
故选:C.
点评:本题主要考查不等式的解法,利用函数奇偶性的性质是解决本题的关键,综合考查函数的奇偶性和单调性的应用.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
曲线y=ex+1在点A(0,1)处的切线斜率为( )
| A、1 | ||
| B、2 | ||
| C、e | ||
D、
|
函数f(x)=sinx+
在区间[0,+∞)内( )
| x |
| A、没有零点 |
| B、有且仅有1个零点 |
| C、有且仅有2个零点 |
| D、有且仅有3个零点 |
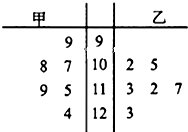 在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如茎叶图所示:
在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如茎叶图所示: