题目内容
若(x-1)6=a6x6+a5x5+…+a2x2+a1x+a0,则函数f(x)=a2x2+a1x+a0的增函数区间为 .
考点:二项式系数的性质
专题:二项式定理
分析:由题意可得函数f(x)=15x2-6x+1,显然函数f(x)为二次函数,且图象的对称轴方程为x=
,由此可得函数f(x)的增区间.
| 1 |
| 5 |
解答:
解:由题意可得函数f(x)=a2x2+a1x+a0 =
x2-
x+
=15x2-6x+1,
显然函数f(x)为二次函数,图象的对称轴方程为x=
,
故函数f(x)的增区间为(
,+∞),
故答案为:(
,+∞).
| C | 4 6 |
| C | 5 6 |
| C | 6 6 |
显然函数f(x)为二次函数,图象的对称轴方程为x=
| 1 |
| 5 |
故函数f(x)的增区间为(
| 1 |
| 5 |
故答案为:(
| 1 |
| 5 |
点评:本题主要考查二项式定理,求展开式中某项的系数,二次函数的性质,属于中档题.

练习册系列答案
相关题目
已知定义域为R的函数y=f(x)在[0,7]上只有l和3两个零点,且y=f(2-x)与y=f (7+x)都是偶函数,则函数y=f(x)在[0,2013]上的零点个数为( )
| A、402 | B、403 |
| C、404 | D、405 |
设f(x)是定义在R上的奇函数,当x<0时,f′(x)>0,且f(-1)=0,则不等式f(x)<0的解集为 ( )
| A、{x|x<-1} |
| B、{x|0<x<1} |
| C、{x|x<-1或0<x<1} |
| D、{x|x≥1或-1<x<0} |
代数式
+
+
的所有可能的值有( )
| a |
| |a| |
| b |
| |b| |
| ab |
| |ab| |
| A、2个 | B、3个 | C、4个 | D、无数个 |
 已知,如图,AB是圆柱的母线,BC是圆柱底面圆的直径,D是圆柱底面圆上与B、C不重合的点,用<MN,EF>表示直线MN、EF的夹角.
已知,如图,AB是圆柱的母线,BC是圆柱底面圆的直径,D是圆柱底面圆上与B、C不重合的点,用<MN,EF>表示直线MN、EF的夹角.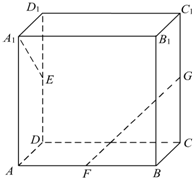 如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成角的余弦值是( )
如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成角的余弦值是( )