题目内容
曲线y=ex+1在点A（0，1）处的切线斜率为（ ）
| A、1 | ||
| B、2 | ||
| C、e | ||
D、
|
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：先求出导数，然后再把x=0代入求值即可求出切线的斜率．
解答：
解：由题意得，y′=ex，
则在点A（0，1）处的切线斜率k=e0=1，
故选A．
则在点A（0，1）处的切线斜率k=e0=1，
故选A．
点评：本题考查了导数的几何意义，即点A处的切线的斜率是该点处的导数值，属于基础题．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
设f（x）是定义在R上的奇函数，当x＜0时，f′（x）＞0，且f（-1）=0，则不等式f（x）＜0的解集为 （ ）
| A、{x|x＜-1} |
| B、{x|0＜x＜1} |
| C、{x|x＜-1或0＜x＜1} |
| D、{x|x≥1或-1＜x＜0} |
定义在R上的函数f(x)=e|x|+x
，且f（x+t）＞f（x）在x∈（-1，+∞）上恒成立，则关于x的方程f（x）=f（t）-e的根的个数叙述正确的是（ ）
| 4 |
| 3 |
| A、有两个 | B、有一个 |
| C、没有 | D、上述情况都有可能 |
已知，如图，AB是圆柱的母线，BC是圆柱底面圆的直径，D是圆柱底面圆上与B、C不重合的点，用＜MN，EF＞表示直线MN、EF的夹角．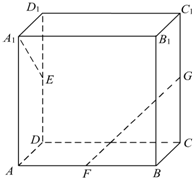
如图，长方体ABCD-A1B1C1D1中，AA1=AB=2，AD=1，点E、F、G分别是DD1、AB、CC1的中点，则异面直线A1E与GF所成角的余弦值是（ ）