题目内容
10.若$\frac{1-tanθ}{1+tanθ}$=3-2$\sqrt{2}$,求$\frac{(sinθ+cosθ)^{2}-1}{cotθ-sinθ•cosθ}$的值.分析 先求出tanθ=$\frac{\sqrt{2}}{2}$,由此利用同角三角函数关系式能求出$\frac{(sinθ+cosθ)^{2}-1}{cotθ-sinθ•cosθ}$的值.
解答 解:∵$\frac{1-tanθ}{1+tanθ}$=3-2$\sqrt{2}$,∴tanθ=$\frac{\sqrt{2}}{2}$,∴sin2θ=$\frac{1}{3}$,
∴$\frac{(sinθ+cosθ)^{2}-1}{cotθ-sinθ•cosθ}$=$\frac{1+2sinθcosθ-1}{cotθ-sinθcosθ}$
=$\frac{2sinθcosθ}{cotθ-sinθcosθ}$=$\frac{2}{\frac{1}{si{n}^{2}θ}-1}$
=$\frac{2}{3-1}$
=1.
点评 本题考查三角函数值的求法,是中档题,解题时要认真审题,注意同角三角函数性质的合理运用.

练习册系列答案
相关题目
1.(1+x)+(1+x)2+(1+x)3+(1+x)4+…+(1+x)49展开式中x3的系数是( )
| A. | ${C}_{51}^{3}$ | B. | ${C}_{50}^{4}$ | C. | ${C}_{51}^{4}$ | D. | ${C}_{47}^{4}$ |
19.已知全集U=R,集合A={x|-2≤x<0},B={x|2x-1<$\frac{1}{4}$},则A∩B=( )
| A. | (-∞,-2)∪(-1,+∞) | B. | (-∞,-2)∪[-1,+∞) | C. | [-2,-1) | D. | (-2,+∞) |
20.已知变量x,y满足$\left\{{\begin{array}{l}{x-2y+4≥0}\\{x≤2}\\{x+y-2≥0}\end{array}}\right.$,则z=x2+y2+2x+2y的取值范围是( )
| A. | [8,23] | B. | [8,25] | C. | [6,23] | D. | [6,25] |
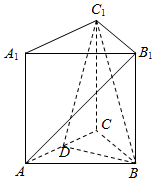 如图,在三棱柱ABC-A1B1C1中,C1C⊥底面ABC,CC1=AB=AC=BC=4,D为线段AC的中点.
如图,在三棱柱ABC-A1B1C1中,C1C⊥底面ABC,CC1=AB=AC=BC=4,D为线段AC的中点.