题目内容
1．（1+x）+（1+x）2+（1+x）3+（1+x）4+…+（1+x）49展开式中x3的系数是（ ）| A． | ${C}_{51}^{3}$ | B． | ${C}_{50}^{4}$ | C． | ${C}_{51}^{4}$ | D． | ${C}_{47}^{4}$ |
分析 根据题意得出（1+x）+（1+x）2+（1+x）3+（1+x）4+…+（1+x）49展开式中x3的系数是${C}_{3}^{3}$+${C}_{4}^{3}$+${C}_{5}^{3}$+…+${C}_{49}^{3}$=${C}_{4}^{4}$+${C}_{4}^{3}$+${C}_{5}^{3}$+…+${C}_{49}^{3}$，利用组合数的性质求值即可．
解答 解：（1+x）+（1+x）2+（1+x）3+（1+x）4+…+（1+x）49展开式中x3的系数是
${C}_{3}^{3}$+${C}_{4}^{3}$+${C}_{5}^{3}$+…+${C}_{49}^{3}$=${C}_{4}^{4}$+${C}_{4}^{3}$+${C}_{5}^{3}$+…+${C}_{49}^{3}$
=${C}_{5}^{4}$+${C}_{5}^{3}$+…+${C}_{49}^{3}$
=${C}_{6}^{4}$+…+${C}_{49}^{3}$
=..=${C}_{49}^{4}$+${C}_{49}^{3}$=${C}_{50}^{4}$．
故选：B．
点评 本题考查了二项式定理的应用问题，也考查了组合数的性质与应用问题，是基础题目．
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
6．sin20°cos40°+sin70°sin140°的值等于（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{4}$ |
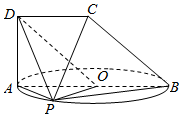如图，梯形ABCD所在平面与以AB为直径的圆所在平面垂直，O为圆心，AB∥CD，∠BAD=90°，AB=2CD．若点P是⊙O上不同于A，B的任意一点．