题目内容
18.已知tan($\frac{π}{4}$+θ)=3,求$\frac{1+sin4θ-cos4θ}{1+sin4θ+cos4θ}$+$\frac{1+sin4θ+cos4θ}{1+sin4θ-cos4θ}$的值.分析 利用正切加法定理求出tanθ=$\frac{1}{2}$,再由正切二倍角公式求出tan2θ═$\frac{4}{3}$,由此利用正弦函数二倍角公式和余弦函数二倍角公式能求出结果.
解答 解:∵tan($\frac{π}{4}$+θ)=$\frac{tan\frac{π}{4}+tanθ}{1-tan\frac{π}{4}tanθ}$=$\frac{1+tanθ}{1-tanθ}$=3,
∴tanθ=$\frac{1}{2}$,∴tan2θ=$\frac{2tanθ}{1-ta{n}^{2}θ}$=$\frac{1}{1-\frac{1}{4}}$=$\frac{4}{3}$,
∴$\frac{1+sin4θ-cos4θ}{1+sin4θ+cos4θ}$+$\frac{1+sin4θ+cos4θ}{1+sin4θ-cos4θ}$
=$\frac{1+2sin2θcos2θ-1+2si{n}^{2}2θ}{1+2sin2θcos2θ+2co{s}^{2}2θ-1}$+$\frac{1+2sin2θcos2θ+2co{s}^{2}2θ-1}{1+2sin2θcos2θ-1+2si{n}^{2}2θ}$
=$\frac{2sin2θ(cos2θ+sin2θ)}{2cos2θ(sin2θ+cos2θ)}$+$\frac{2cos2θ(sin2θ+cos2θ)}{2sin2θ(cos2θ+sin2θ)}$
=tan2θ+cot2θ
=$\frac{4}{3}+\frac{3}{4}$
=$\frac{25}{12}$.
点评 本题考查三角函数值的求法,是中档题,解题时要认真审题,注意三角函数加法定理和二倍角公式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.sin20°cos40°+sin70°sin140°的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
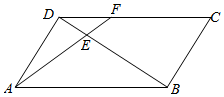 如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.
如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.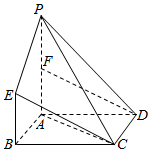 如图,矩形ABCD中,BC=2,AB=1,PA⊥平面ABCD,BE∥PA,BE=$\frac{1}{2}$PA,F为PA的中点.
如图,矩形ABCD中,BC=2,AB=1,PA⊥平面ABCD,BE∥PA,BE=$\frac{1}{2}$PA,F为PA的中点.