题目内容
20.已知变量x,y满足$\left\{{\begin{array}{l}{x-2y+4≥0}\\{x≤2}\\{x+y-2≥0}\end{array}}\right.$,则z=x2+y2+2x+2y的取值范围是( )| A. | [8,23] | B. | [8,25] | C. | [6,23] | D. | [6,25] |
分析 作出不等式组对应的平面区域,利用z的几何意义,结合两点间的距离公式进行求解即可.
解答 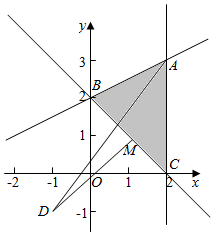 解:z=x2+y2+2x+2y=(x+1)2+(y+1)2-2,
解:z=x2+y2+2x+2y=(x+1)2+(y+1)2-2,
设m=(x+1)2+(y+1)2,则m的几何意义是区域内的点到点D(-1,-1)的距离的平方,
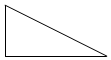
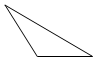
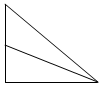
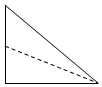
作出不等式组对应的平面区域如图,
则点D到直线x+y-2=0的距离最小,此时d=$\frac{|-1-1-2|}{\sqrt{2}}=\frac{4}{\sqrt{2}}$=2$\sqrt{2}$,
AD的距离最大,由$\left\{\begin{array}{l}{x=2}\\{x-2y+4=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,即A(2,3),
则AD=$\sqrt{(2+1)^{2}+(3+1)^{2}}$=$\sqrt{9+16}=\sqrt{25}$=5,
即(2$\sqrt{2}$)2≤m≤25,即8≤m≤25,
则6≤m-2≤23,
即6≤z≤23,
故选:C.
点评 本题主要考查线性规划的应用,根据零点间的距离公式,结合数形结合是解决本题的关键.

练习册系列答案
相关题目
15.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,-3).若向量$\overrightarrow{c}$满足$\overrightarrow{c}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$),且$\overrightarrow{b}$∥($\overrightarrow{a}$-$\overrightarrow{c}$),则$\overrightarrow{c}$=( )
| A. | $(\frac{7}{9},\frac{7}{3})$ | B. | $(-\frac{7}{9},\frac{7}{3})$ | C. | $(\frac{7}{9},-\frac{7}{3})$ | D. | $(-\frac{7}{9},-\frac{7}{3})$ |
12.已知全集U=R,集合A={x|x<-1或x>4),B={x|-2≤x≤3),那么阴影部分表示的集合为( )
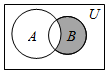

| A. | {x|-2≤x<4} | B. | {x|x≤3或x≥4} | C. | {x|-2≤x≤一1} | D. | {x|-1≤x≤3} |
9.若函数f(x)=ln(x+$\sqrt{a+{x}^{2}}$)为奇函数,则a=( )
| A. | -1 | B. | 0 | C. | 1 | D. | -1或1 |
10.若双曲线的顶点和焦点分别为椭圆$\frac{{x}^{2}}{2}$+y2=1的焦点和顶点,则该双曲线方程为( )
| A. | x2-y2=1 | B. | $\frac{{x}^{2}}{2}$-y2=1 | C. | x2-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 |
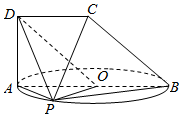 如图,梯形ABCD所在平面与以AB为直径的圆所在平面垂直,O为圆心,AB∥CD,∠BAD=90°,AB=2CD.若点P是⊙O上不同于A,B的任意一点.
如图,梯形ABCD所在平面与以AB为直径的圆所在平面垂直,O为圆心,AB∥CD,∠BAD=90°,AB=2CD.若点P是⊙O上不同于A,B的任意一点.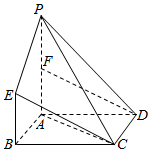 如图,矩形ABCD中,BC=2,AB=1,PA⊥平面ABCD,BE∥PA,BE=$\frac{1}{2}$PA,F为PA的中点.
如图,矩形ABCD中,BC=2,AB=1,PA⊥平面ABCD,BE∥PA,BE=$\frac{1}{2}$PA,F为PA的中点.