题目内容
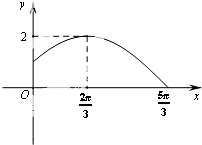 已知函数f(x)=
已知函数f(x)=
|
| π |
| 2 |
| 5π |
| 3 |
(Ⅰ)求f(x)的在区间(0,
| 5π |
| 3 |
(Ⅱ)若f(x)=m恒有实数解,求实数m的取值范围.
考点:函数的图象,函数解析式的求解及常用方法,函数的零点
专题:函数的性质及应用
分析:(Ⅰ)由图象知A=2,T=4(
-
)=4π,故ω=
=
,因此f(x)=2sin(
x+Φ),根据(
,2)是五点法作图中的第二点求出Φ,
(Ⅱ)方程f(x)=m恒有实数解?m∈{f(x)|x∈[-4,
]},有两种方法:法一,分两段讨论解方程;法二,画出f(x)的图象,结合图象解题.
| 5π |
| 3 |
| 2π |
| 3 |
| 2π |
| T |
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
(Ⅱ)方程f(x)=m恒有实数解?m∈{f(x)|x∈[-4,
| 5π |
| 3 |
解答:
解:(Ⅰ)由图象知A=2,T=4(
-
)=4π,∴ω=
=
,
∴f(x)=2sin(
x+Φ)
由图象知:(
,2)是五点法作图中的第二点,
∴
×
+ϕ=
即ϕ=
,
∴f(x)=2sin(
x+
),x∈(0,
].
(Ⅱ)方程f(x)=m恒有实数解?m∈{f(x)|x∈[-4,
]},
①当x∈(0,
]时,由图象可知f(x)∈[0,2],
②当x∈[-4,0]时,f(x)=x2+4x+1=(x+2)2-3,
∴f(x)min=f(-2)=-3,f(x)max=f(-4)=f(0)=1,
∴此时f(x)∈[-3,1],
综上所述,函数f(x)的值域为[-3,2],
∴f(x)=m恒有实数解时,实数m的取值范围为[-3,2].
解法二:方程f(x)=m恒有实数解?m∈{f(x)|x∈[-4,
]},
在同一坐标系中作出函数f(x)在x∈[-4,0]上的图象如下,
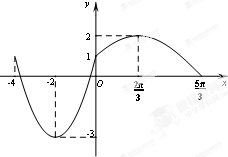
由图象可知函数f(x)的值域为[-3,2],
∴f(x)=m恒有实数解时,实数m的取值范围为[-3,2].
| 5π |
| 3 |
| 2π |
| 3 |
| 2π |
| T |
| 1 |
| 2 |
∴f(x)=2sin(
| 1 |
| 2 |
由图象知:(
| 2π |
| 3 |
∴
| 1 |
| 2 |
| 2π |
| 3 |
| π |
| 2 |
| π |
| 6 |
∴f(x)=2sin(
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 3 |
(Ⅱ)方程f(x)=m恒有实数解?m∈{f(x)|x∈[-4,
| 5π |
| 3 |
①当x∈(0,
| 5π |
| 3 |
②当x∈[-4,0]时,f(x)=x2+4x+1=(x+2)2-3,
∴f(x)min=f(-2)=-3,f(x)max=f(-4)=f(0)=1,
∴此时f(x)∈[-3,1],
综上所述,函数f(x)的值域为[-3,2],
∴f(x)=m恒有实数解时,实数m的取值范围为[-3,2].
解法二:方程f(x)=m恒有实数解?m∈{f(x)|x∈[-4,
| 5π |
| 3 |
在同一坐标系中作出函数f(x)在x∈[-4,0]上的图象如下,

由图象可知函数f(x)的值域为[-3,2],
∴f(x)=m恒有实数解时,实数m的取值范围为[-3,2].
点评:本题主要考查分段函数的性质,分情况讨论是解决分段函数有关问题的关键,答题时应仔细认真.

练习册系列答案
相关题目
已知全集U=R,集合A={x|lgx≤0},B={x|2x<
},则A∩B=( )
| 3 | 2 |
A、(0,
| ||
B、(0,
| ||
C、[
| ||
D、(-∞,
|
已知点(x,y)是不等式组
,表示的 平面区域的一个动点,且目标函数z=2x+y的最大值为7,最小值为1,则
的取值范围是( )
|
4y-
| ||
x+
|
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
下列各式的因式分解中正确的是( )
| A、-a2+ab-ac=-a(a+b-c) | ||||||
| B、9xy-6x2y2=3xy(3-2xy) | ||||||
| C、3a2x-6bx+3x=3x(a2-2b) | ||||||
D、
|