题目内容
已知矩形ABCD的对角线交于点P(2,0),边AB所在直线的方程为x-3y-6=0,点T(-1,1)在边AD所在的直线上.
(1)求矩形ABCD的外接圆P的方程;
(2)△AEF是圆P的内接三角形,其重心G的坐标是(1,1),求直线EF的方程.
(1)求矩形ABCD的外接圆P的方程;
(2)△AEF是圆P的内接三角形,其重心G的坐标是(1,1),求直线EF的方程.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)根据对角线的性质以及直线方程即可求矩形ABCD的外接圆P的方程;
(2)根据三角形重心的性质,即可得到结论.
(2)根据三角形重心的性质,即可得到结论.
解答:
解:(1)设A点的坐标为(x,y),∵KAB=
且AB⊥AD,
∴KAD=-3,又T(-1,1)在AD上,
∴
,∴
,
即A点坐标为(0,-2),
又P点是矩形ABCD两条对角线的交点,
∴P点(2,0)即为矩形ABCD外接圆的圆心,其半径r=|PA|=2
,
即圆P的方程为(x-2)2+y2=8.
(2)连AG延长交BC于点M(x0,y0)(3),则M点是EF的中点,连PM
∵G是△AEF的重心,
∴
=2
,
∴(1,3)=2(x0-1,y0-1),解得
,
∵P是圆心,M是EF中点∴PM⊥EF且KPM=-5
∴KEF=
,
即直线EF的方程为y-
=
(x-
),
即x-5y+11=0.
| 1 |
| 3 |
∴KAD=-3,又T(-1,1)在AD上,
∴
|
|
即A点坐标为(0,-2),
又P点是矩形ABCD两条对角线的交点,
∴P点(2,0)即为矩形ABCD外接圆的圆心,其半径r=|PA|=2
| 2 |
即圆P的方程为(x-2)2+y2=8.
(2)连AG延长交BC于点M(x0,y0)(3),则M点是EF的中点,连PM
∵G是△AEF的重心,
∴
| AG |
| GM |
∴(1,3)=2(x0-1,y0-1),解得
|
∵P是圆心,M是EF中点∴PM⊥EF且KPM=-5
∴KEF=
| 1 |
| 5 |
即直线EF的方程为y-
| 5 |
| 2 |
| 1 |
| 5 |
| 3 |
| 2 |
即x-5y+11=0.
点评:本题主要考查圆的方程的求解以及直线方程的应用,综合考查直线的求解.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
已知双曲线
-y2=1(a>0)的实轴长、虚轴长、焦距长成等差数列,则双曲线的渐近线方程为( )
| x2 |
| a2 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
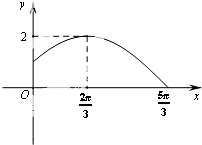 已知函数f(x)=
已知函数f(x)=