题目内容
已知0<α<
,cosα=
,tanβ=
.求下列式子的值:
(1)tanα;
(2)cos(π-α)-sin(α+
);
(3)tan(α-2β).
| π |
| 2 |
| 3 |
| 5 |
| 1 |
| 3 |
(1)tanα;
(2)cos(π-α)-sin(α+
| π |
| 2 |
(3)tan(α-2β).
考点:两角和与差的正切函数,运用诱导公式化简求值
专题:三角函数的求值
分析:(1)依题意,利用sin2α+cos2α=1,即可求得sinα=
=
,继而可得tanα;
(2)利用cosα=
及诱导公式即可求得cos(π-α)-sin(α+
);
(3)利用二倍角的正切及两角差的正切公式即可求得tan(α-2β)的值.
| 1-cos2α |
| 4 |
| 5 |
(2)利用cosα=
| 3 |
| 5 |
| π |
| 2 |
(3)利用二倍角的正切及两角差的正切公式即可求得tan(α-2β)的值.
解答:
(本小题满分12分)
解:(1)∵sin2α+cos2α=1,0<α<
,cosα=
,
∴sinα=
=
,
∴tanα=
; …(4分)
(2)cos(π-α)-sin(α+
)=-cosα-cosα=-
; …(8分)
(3)∵tanβ=
,∴tan2β=
=
=
.…(10分)
∴tan(α-2β)=
=
=
.…(12分)
解:(1)∵sin2α+cos2α=1,0<α<
| π |
| 2 |
| 3 |
| 5 |
∴sinα=
| 1-cos2α |
| 4 |
| 5 |
∴tanα=
| 4 |
| 3 |
(2)cos(π-α)-sin(α+
| π |
| 2 |
| 6 |
| 5 |
(3)∵tanβ=
| 1 |
| 3 |
| 2tanβ |
| 1-tan2β |
2×
| ||
1-(
|
| 3 |
| 4 |
∴tan(α-2β)=
| tanα-tan2β |
| 1+tanαtan2β |
| ||||
1+
|
| 7 |
| 24 |
点评:本题考查运用诱导公式化简求值,着重考查三角函数间的关系式及二倍角的正切与两角差的正切公式的应用,属于中档题.

练习册系列答案
相关题目
已知双曲线
-y2=1(a>0)的实轴长、虚轴长、焦距长成等差数列,则双曲线的渐近线方程为( )
| x2 |
| a2 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
已知函数f(x)的图象如图所示,则它的一个可能的解析式为( )
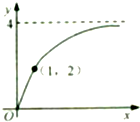

A、y=2
| ||
B、y=2x
| ||
| C、y=log2(x+3) | ||
D、y=4-
|
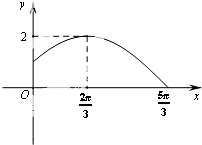 已知函数f(x)=
已知函数f(x)=