题目内容
已知数列{an}满足a1=1,an+1=2an+(-1)n(n∈N*).
(1)若bn=a2n-1-
,求证:数列{bn}是等比数列并求其通项公式;
(2)求数列{an}的通项公式;
(3)求证:
+
+…+
<3.
(1)若bn=a2n-1-
| 1 |
| 3 |
(2)求数列{an}的通项公式;
(3)求证:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
考点:数列与不等式的综合,数列的求和,等比数列的性质,数列递推式
专题:等差数列与等比数列
分析:(1)利用已知递推关系式推出a2n+1=4a2n-1-1,然后证明
=4,即可证明数列{bn}是等比数列,即可求其通项公式;
(2)利用(1)两个数列的关系式,通过n为奇数与偶数求数列{an}的通项公式;
(3)通过n为奇数与偶数分别求解
+
+…+
的和,然后判断与3的大小关系即可..
| bn+1 |
| bn |
(2)利用(1)两个数列的关系式,通过n为奇数与偶数求数列{an}的通项公式;
(3)通过n为奇数与偶数分别求解
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
解答:
(本小题满分15分)
解:(1)a2n+1=2a2n+(-1)2n=2[2a2n-1+(-1)2n-1]+1=4a2n-1-1,…(2分)
=
=
=4,又b1=a1-
=
.
所以{bn}是首项为
,公比为4的等比数列,且bn=
×4n-1.…(5分)
(2)由(1)可知a2n-1=bn+
=
×4n-1+
=
(22n-1+1),…(7分)a2n=2a2n-1+(-1)2n-1=
(22n-1+1)-1=
(22n-1).…(9分)
所以an=
(2n+(-1)n+1),
或an=
…(10分)
(3)∴a2n=
•22n-
,a2n-1=
•22n-1+
.
+
=
+
=
=
≤
=3(
+
)…(12分)
当n=2k时,(
+
)+(
+
)+…+(
+
)
≤3(
+
+
+…+
)=3×
=3-
<3
当n=2k-1时,(
+
)+(
+
)+…+(
+
)+
<(
+
)+(
+
)+…+(
+
)<3
∴
+
+…+
<3.…(15分)
解:(1)a2n+1=2a2n+(-1)2n=2[2a2n-1+(-1)2n-1]+1=4a2n-1-1,…(2分)
| bn+1 |
| bn |
a2n+1-
| ||
a2n-1-
|
4a2n-1-
| ||
a2n-1-
|
| 1 |
| 3 |
| 2 |
| 3 |
所以{bn}是首项为
| 2 |
| 3 |
| 2 |
| 3 |
(2)由(1)可知a2n-1=bn+
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
所以an=
| 1 |
| 3 |
或an=
|
(3)∴a2n=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| a2n-1 |
| 1 |
| a2n |
| 3 |
| 22n-1+1 |
| 3 |
| 22n-1 |
=
| 3×(22n+22n-1) |
| 22n-1•22n+22n-22n-1-1 |
=
| 3×(22n+22n-1) |
| 22n-1•22n+22n-1-1 |
| 3×(22n+22n-1) |
| 22n-1•22n |
=3(
| 1 |
| 22n-1 |
| 1 |
| 22n |
当n=2k时,(
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a2k-1 |
| 1 |
| a2k |
≤3(
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 22k |
| ||||
1-
|
=3-
| 3 |
| 22k |
当n=2k-1时,(
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a2k-3 |
| 1 |
| a2k-2 |
| 1 |
| a2k-1 |
<(
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a2k-1 |
| 1 |
| a2k |
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
点评:本题考查数列的递推关系式的应用,数列的通项公式的求法,前n项和的求法,数列与不等式的关系,考查分类讨论思想的应用,考查计算能力.

练习册系列答案
相关题目
已知l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )
| A、若l⊥α,m?α,则l⊥m |
| B、若l⊥m,m?α,则l⊥α |
| C、若l∥α,m?α,则l∥m |
| D、若l∥α,m∥α,则l∥m |
用an表示正整数n的最大奇因数(如a3=3、a10=5),记数列{an}的前n项的和为Sn,则S64值为( )
| A、342 | B、1366 |
| C、2014 | D、5462 |
已知双曲线
-y2=1(a>0)的实轴长、虚轴长、焦距长成等差数列,则双曲线的渐近线方程为( )
| x2 |
| a2 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
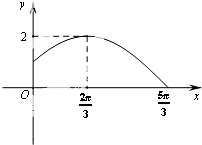 已知函数f(x)=
已知函数f(x)=