题目内容
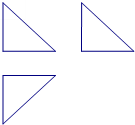
如图,某三棱锥的三视图都是直角边为2的等腰直角三角形,则该三棱锥的体积是 .

考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:先由三视图判断出几何体的形状及度量长度,然后利用三棱锥的体积公式求出该几何体的体积.
解答:
解:由三视图得,该几何体为底面为直角边边长为2的等腰直角三角形,
两个相邻的侧面也是直角边边长为2的等腰直角三角形,则高为2.
∴该几何体的体积为V=
×
×2×2×2=
.
故答案为:
.
两个相邻的侧面也是直角边边长为2的等腰直角三角形,则高为2.
∴该几何体的体积为V=
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:解决三视图的题目,关键是由三视图判断出几何体的形状及度量长度,然后利用几何体的面积及体积公式解决.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
用an表示正整数n的最大奇因数(如a3=3、a10=5),记数列{an}的前n项的和为Sn,则S64值为( )
| A、342 | B、1366 |
| C、2014 | D、5462 |
下列各组函数中为同一函数的是( )
A、y=(
| ||||||
B、y=|x|与y=
| ||||||
C、f(x)=
| ||||||
| D、y=x与y=a logax |
下列命题错误的是( )
| A、命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R均有x2+x+1≥0” | ||||||||
| B、若p∧q为假命题,则p,q均为假命题 | ||||||||
C、若a,b∈[0,1],则不等式a2+b2<
| ||||||||
D、“平面向量
|
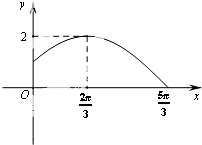 已知函数f(x)=
已知函数f(x)=