题目内容
某产品共有三个等级,分别为一等品、二等品和不合格品.从一箱产品中随机抽取1件进行检测,设“抽到一等品”的概率为0.65,“抽到二等品”的概率为0.3,则“抽到不合格品”的概率为( )
| A、0.95 | B、0.7 |
| C、0.35 | D、0.05 |
考点:概率的基本性质,互斥事件与对立事件,互斥事件的概率加法公式
专题:计算题,概率与统计
分析:根据题意,分析可得“抽到一等品”与“抽到二等品”是互斥事件,结合题意可得P(A+B),“抽到不合格品”与“抽到一等品或二等品”是对立事件,由对立事件的概率计算可得答案.
解答:
解:根据题意,记“抽到一等品”为事件A,“抽到二等品”为事件B,“抽到不合格品”为事件C,
分析可得“抽到一等品”与“抽到二等品”是互斥事件,
P(A+B)=0.65+0.3=0.95,
“抽到不合格品”与“抽到一等品或二等品”是对立事件,
P(C)=1-P(A+B)=1-0.95=0.05.
故选D.
分析可得“抽到一等品”与“抽到二等品”是互斥事件,
P(A+B)=0.65+0.3=0.95,
“抽到不合格品”与“抽到一等品或二等品”是对立事件,
P(C)=1-P(A+B)=1-0.95=0.05.
故选D.
点评:本题考查事件之间的关系,注意区分“互斥事件”与“对立事件”的区别与联系.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积是( )


| A、12 | B、36 | C、24 | D、72 |
已知(1+i)(1-mi)是实数(i是虚数单位),则实数m的值为( )
| A、±1 | B、1 | C、-1 | D、0 |
设集合A={x|y=lg(x-2)},B={y|y=2x-1,x∈A},则∁RA∪B( )
| A、(2,+∞) | B、[2,+∞) |
| C、∅ | D、R |
对于四个命题p,q,r,m:已知p是q的充分条件,r是q的必要条件,p是r的充要条件,r是m的只充分条件,则m是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
若f(x)是R上的奇函数,则2f(0)的值等于( )
| A、0 | B、1 | C、2 | D、4 |
已知
=-2,则tanx的值为( )
| 1-cosx+sinx |
| 1+cosx+sinx |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
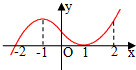 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: