题目内容
设fn(x)=sin(
+x)(n∈N*),若△ABC的内角A满足f1(A)+f2(A)+…+f2014(A)=0,则sinA+cosA= .
| nπ |
| 2 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:分别取n=1,2,3,4,5求得fn(x),发现函数周期性出现的规律,再由f1(A)+f2(A)+…+f2014(A)=0得到cosA-sinA=0,求出角A的值,则答案可求.
解答:
解:由fn(x)=sin(
+x),得:
f1(x)=sin(
+x)=cosx,
f2(x)=sin(π+x)=-sinx,
f3(x)=sin(
+x)=-cosx,
f4(x)=sin(2π+x)=sinx,
f5(x)=sin(
+x)=cosx,
…
fn(x)周期出现,周期为4,
由f1(A)+f2(A)+…+f2014(A)=0,得:
cosA-sinA=0,即tanA=1,
∵0<A<π,
∴A=
.
∴sinA+cosA=sin
+cos
=
+
=
.
故答案为:
.
| nπ |
| 2 |
f1(x)=sin(
| π |
| 2 |
f2(x)=sin(π+x)=-sinx,
f3(x)=sin(
| 3π |
| 2 |
f4(x)=sin(2π+x)=sinx,
f5(x)=sin(
| 5π |
| 2 |
…
fn(x)周期出现,周期为4,
由f1(A)+f2(A)+…+f2014(A)=0,得:
cosA-sinA=0,即tanA=1,
∵0<A<π,
∴A=
| π |
| 4 |
∴sinA+cosA=sin
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 2 |
故答案为:
| 2 |
点评:本题考查利用三角函数的诱导公式化简求值,解答此题的关键在于发现函数具备周期性,是中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
某社区对该区所辖的老年人是否需要特殊照顾进行了一项分性别的抽样调查,针对男性老年人和女性老年人需要特殊照顾和不需要特殊照顾得出了一个2×2的列联表,并计算得出k=4.350,则下列结论正确的是( )
| A、有95%的把握认为该社区的老年人是否需要特殊照顾与性别有关 |
| B、有95%的把握认为该社区的老年人是否需要特殊照顾与性别无关 |
| C、该社区需要特殊照顾的老年人中有95%是男性 |
| D、该地区每100名老年人中有5个需要特殊照顾 |
已知(1+i)(1-mi)是实数(i是虚数单位),则实数m的值为( )
| A、±1 | B、1 | C、-1 | D、0 |
若复数
(m∈R)的实部与虚部的和为零,则m的值等于( )
| 2+mi |
| 1+i |
| A、0 | B、1 | C、2 | D、3 |
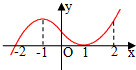 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: