题目内容
曲线C是平面内到两条定直线x=0,y=0距离之和为8的点的轨迹.给出下列四个结论:
①曲线C关于y轴对称;
②曲线C关于原点对称;
③曲线C上任意一点P在x轴上的投影点为P′,则|OP′|≤8;
④曲线C与x轴,y轴在第一象限内围成的图象的面积为16(3
-2).
以上结论中正确的序号是 (写出所有正确结论的序号).
①曲线C关于y轴对称;
②曲线C关于原点对称;
③曲线C上任意一点P在x轴上的投影点为P′,则|OP′|≤8;
④曲线C与x轴,y轴在第一象限内围成的图象的面积为16(3
| 2 |
以上结论中正确的序号是
考点:轨迹方程
专题:直线与圆,简易逻辑
分析:设曲线C上的动点P(x,y),由题意求得曲线C的方程,去绝对值后画出图形,数形结合可判断四个命题的真假.
解答:
解:设曲线C上的动点P(x,y),
由P到两条定直线x=0,y=0距离之和为8得:
|x|+|y|=8.
去绝对值得:
,
∴曲线C的轨迹如图:
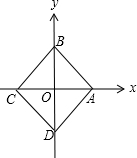
由图可知,曲线C关于y轴对称,命题①正确;
曲线C关于原点对称,命题②正确;
曲线C上任意一点P在x轴上的投影点为P′均落在线段AC上,
∴|OP′|≤8,命题③正确;
曲线C与x轴,y轴在第一象限内围成的图象的面积为S=
×8×8=32,命题④错误.
∴正确结论的序号是①②③.
故答案为:①②③.
由P到两条定直线x=0,y=0距离之和为8得:
|x|+|y|=8.
去绝对值得:
|
∴曲线C的轨迹如图:

由图可知,曲线C关于y轴对称,命题①正确;
曲线C关于原点对称,命题②正确;
曲线C上任意一点P在x轴上的投影点为P′均落在线段AC上,
∴|OP′|≤8,命题③正确;
曲线C与x轴,y轴在第一象限内围成的图象的面积为S=
| 1 |
| 2 |
∴正确结论的序号是①②③.
故答案为:①②③.
点评:本题考查命题的真假判断与应用,考查了轨迹方程的求法,解答的关键在于正确作出图形,是中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
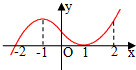 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: