题目内容
函数f(x)在[a,b]区间上的值域仍为[a,b],则区间[a,b]称为函数f(x)的一个的保值区间,函数y=2sinx的保值区间个数为 .
考点:正弦函数的定义域和值域
专题:函数的性质及应用,三角函数的求值
分析:由保值区间的定义,结合函数y=2sinx的值域是[-2,2],可得[a,b]⊆[-2,2],考虑函数y=2sinx在区间[a,b]上单调性,结合a<b即可得到函数y的“保值”区间.
解答:
解:在同一坐标系中作出函数y=2sinx和函数y=x的图象如下图所示:

由图可知:函数y=2sinx的保值区间有:
[-2,0],[0,2],[-2,2]共3个,
故答案为:3

由图可知:函数y=2sinx的保值区间有:
[-2,0],[0,2],[-2,2]共3个,
故答案为:3
点评:本题考查的知识点是正弦函数的图象和性质,正确理解新定义“保值区间”的含义是解答的关键.

练习册系列答案
相关题目
对于四个命题p,q,r,m:已知p是q的充分条件,r是q的必要条件,p是r的充要条件,r是m的只充分条件,则m是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
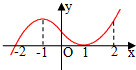 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: