题目内容
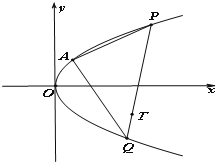如图，已知过点A（1，2）的抛物线C：y2=ax与过点T（3，-2）的动直线l相交于P、Q两点．（Ⅰ）求直线AP与直线AQ的斜率的乘积；
（Ⅱ）若∠APQ=∠AQP，求证：△APQ的周长为定值．
考点：双曲线的简单性质
专题：综合题,圆锥曲线的定义、性质与方程
分析：（Ⅰ）设直线l的方程为x=m（y+2）+3代入抛物线方程，利用韦达定理，结合斜率公式，即可求直线AP与直线AQ的斜率的乘积；
（Ⅱ）求出PQ的中点坐标，可得
=-m，即m3+m2+2m-1=0，构造函数，利用方程m3+m2+2m-1=0有唯一实根，即可证明结论．
（Ⅱ）求出PQ的中点坐标，可得
| 2m-2 |
| 2m2+2m+3-1 |
解答：
（I）解：由抛物线C：y2=ax过点A（1，2）知a=4…（1分）
设直线l的方程为x=m（y+2）+3
代入抛物线方程得y2-4my-8m-12=0 …（2分）
设P（x1，y1），Q（x2，y2），
则y1+y2=4m，y1y2=-8m-12 …（3分）
∴kAPkAQ=
=-2 …（6分）
（II）证明：PQ的中点坐标为（
，
），即（
，
），
∴PQ的中点坐标为（2m2+2m+3，2m），…（8分）
由已知得
=-m，即m3+m2+2m-1=0．…（10分）
设f（m）=m3+m2+2m-1，则f′（m）=3m2+2m+2＞0，
∴f（m）在R上是增函数，又f（0）=-1，f′（1）=3，故f（m）在（0，1）内有一个零点，
函数f（m）有且只有一个零点，即方程m3+m2+2m-1=0有唯一实根．
∴满足条件的三角形唯一确定，从而△APQ的周长为定值．…（14分）
设直线l的方程为x=m（y+2）+3
代入抛物线方程得y2-4my-8m-12=0 …（2分）
设P（x1，y1），Q（x2，y2），
则y1+y2=4m，y1y2=-8m-12 …（3分）
∴kAPkAQ=
| 16 |
| y1y2+2(y1+y2)+4 |
（II）证明：PQ的中点坐标为（
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| ||||
| 2 |
| y1+y2 |
| 2 |
∴PQ的中点坐标为（2m2+2m+3，2m），…（8分）
由已知得
| 2m-2 |
| 2m2+2m+3-1 |
设f（m）=m3+m2+2m-1，则f′（m）=3m2+2m+2＞0，
∴f（m）在R上是增函数，又f（0）=-1，f′（1）=3，故f（m）在（0，1）内有一个零点，
函数f（m）有且只有一个零点，即方程m3+m2+2m-1=0有唯一实根．
∴满足条件的三角形唯一确定，从而△APQ的周长为定值．…（14分）
点评：本题考查抛物线方程，考查直线与抛物线的位置关系，考查导数知识的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
函数f（x）=x-
的零点所在的大致区间是（ ）
| 2 |
| x |
| A、（-4，-2） |
| B、（-2，-1） |
| C、（2，4） |
| D、（4，+∞） |
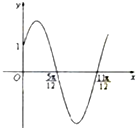已知函数f（x）=Asin（ωx+φ）（x∈R，ω＞0，0＜φ＜
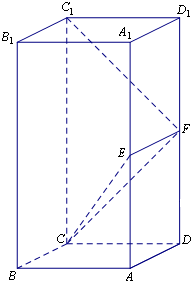在长方体ABCD-A1B1C1D1中，AA1=2AB，E，F分别是AA1，DD1的中点．